 如图,在棱长为4的正方体ABCDA1B1C1D1中,P是A1B1上一点,且PB1=
如图,在棱长为4的正方体ABCDA1B1C1D1中,P是A1B1上一点,且PB1=| 1 |
| 4 |
A、
| ||
B、
| ||
| C、4 | ||
| D、16 |
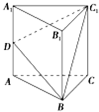 如图,在正三棱柱ABC A1B1C1中,D为棱AA1的中点,若截面三角形BC1D是面积为6的直角三角形,则此三棱柱的体积为( )
如图,在正三棱柱ABC A1B1C1中,D为棱AA1的中点,若截面三角形BC1D是面积为6的直角三角形,则此三棱柱的体积为( )A、16
| ||||
B、8
| ||||
C、4
| ||||
D、
|
 如图,在棱长为4的正方体ABCDA1B1C1D1中,P是A1B1上一点,且PB1=
如图,在棱长为4的正方体ABCDA1B1C1D1中,P是A1B1上一点,且PB1=| 1 |
| 4 |
A、
| ||
B、
| ||
| C、4 | ||
| D、16 |
 如图,在正三棱柱ABC A1B1C1中,D为棱AA1的中点,若截面三角形BC1D是面积为6的直角三角形,则此三棱柱的体积为( )
如图,在正三棱柱ABC A1B1C1中,D为棱AA1的中点,若截面三角形BC1D是面积为6的直角三角形,则此三棱柱的体积为( )A、16
| ||||
B、8
| ||||
C、4
| ||||
D、
|