题目内容
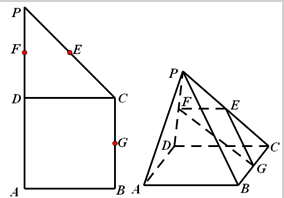 在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,DC=2,∠PCD=45°,D,E,F,G分别为线段PA,PC,PD,BC的中点,现将△PDC折起,使平面PDC⊥平面ABCD(图2).
在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,DC=2,∠PCD=45°,D,E,F,G分别为线段PA,PC,PD,BC的中点,现将△PDC折起,使平面PDC⊥平面ABCD(图2).(1)求证:AP∥平面EFG;
(2)求三棱椎C-EFG的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)证明EF∥平面PAB,同理EG∥平面PAB,从而得到平面PAB∥平面EFG,而PA在平面PAB内,故有PA∥平面EFG.
(2)以D为原点,DA为x轴,DC为y轴,DP为z轴,建立空间直角坐标系,利用向量法能求出三棱椎C-EFG的体积.
(2)以D为原点,DA为x轴,DC为y轴,DP为z轴,建立空间直角坐标系,利用向量法能求出三棱椎C-EFG的体积.
解答:
(1)证明:∵PE=EC,PF=FD,
∴EF是△PDC的中位线,∴EF∥CD.
又CD∥AB,∴EF∥AB,
∴EF∥平面PAB,同理EG∥平面PAB.
又∵EF∩EG=E,
∴平面PAB∥平面EFG,而PA在平面PAB内,
∴PA∥平面EFG.
(2)解:∵BC∥AP,AB⊥BC,CD⊥AP,
平面PDC⊥平面ABCD,
∴AD,DC,DP两两垂直,
以D为原点,DA为x轴,DC为y轴,DP为z轴,
建立空间直角坐标系,
∵DC=2,∠PCD=45°,
D,E,F,G分别为线段PA,PC,PD,BC的中点,
∴C(0,2,0),P(0,0,2),E(0,1,1),
F(0,0,1),G(1,2,0),
=(0,1,0),
=(1,2,-1),
=(1,1,-1),
=(0,2,-1),
设平面EFG的法向量
=(x,y,z),
则
,取x=1,得
=(1,0,1),
点C到平面EFG的距离h=
=
=
,
cos<
,
>=
,∴sin<
,
>=
.
S△EFG=
|
|•|
|•sin<
,
>=
×1×
×
=
,
∴三棱椎C-EFG的体积V=
S△EFG•h=
×
×
=
.

∴EF是△PDC的中位线,∴EF∥CD.
又CD∥AB,∴EF∥AB,
∴EF∥平面PAB,同理EG∥平面PAB.
又∵EF∩EG=E,
∴平面PAB∥平面EFG,而PA在平面PAB内,
∴PA∥平面EFG.
(2)解:∵BC∥AP,AB⊥BC,CD⊥AP,
平面PDC⊥平面ABCD,
∴AD,DC,DP两两垂直,
以D为原点,DA为x轴,DC为y轴,DP为z轴,
建立空间直角坐标系,
∵DC=2,∠PCD=45°,
D,E,F,G分别为线段PA,PC,PD,BC的中点,
∴C(0,2,0),P(0,0,2),E(0,1,1),
F(0,0,1),G(1,2,0),
| FE |
| FG |
| EG |
| FC |
设平面EFG的法向量
| n |
则
|
| n |
点C到平面EFG的距离h=
|
| ||||
|
|
| |-1| | ||
|
| ||
| 2 |
cos<
| FE |
| FG |
| 2 | ||
|
| FE |
| FG |
| ||
| 3 |
S△EFG=
| 1 |
| 2 |
| FE |
| FG |
| FE |
| FG |
| 1 |
| 2 |
| 6 |
| ||
| 3 |
| ||
| 2 |
∴三棱椎C-EFG的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 6 |
点评:本题考查证明线面平行的方法,考查三棱锥的体积的求法,是中档题,解题时要注意向量法的合理运用.

练习册系列答案
相关题目
以-3i+
的虚部为实部,以-3i2+
i的实部为虚部的复数是( )
| 2 |
| 2 |
| A、3-3i | ||||
| B、-3+3i | ||||
C、-
| ||||
D、
|
等比数列{an}中,a6=2,a5=5,则数列{lgan}的前10项和等于( )
| A、6 | B、5 | C、4 | D、3 |
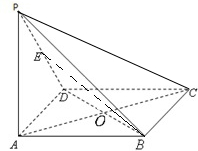 如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=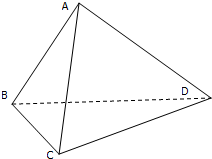 如图所示,空间四边形ABCD中,平面ABD⊥平面BCD,∠BAD=90°,∠BCD=90°,且AB=AD,则AC与平面BCD所成的角为
如图所示,空间四边形ABCD中,平面ABD⊥平面BCD,∠BAD=90°,∠BCD=90°,且AB=AD,则AC与平面BCD所成的角为