用反证法证明命题:“三角形的内角中至少有一个不大于60度”时,假设正确的是( )
| A.假设三个内角都不大于60度 |
| B.假设三个内角都大于60度 |
| C.假设三个内角至多有一个大于60度 |
| D.假设三个内角有两个大于60度 |
如果△A1B1C1的三个内角的余弦值分别等于△A2B2C2的三个内角的正弦值,那么( )
| A.△A1B1C1和△A2B2C2都是锐角三角形 |
| B.△A1B1C1和△A2B2C2都是钝角三角形 |
| C.△A1B1C1是钝角三角形,△A2B2C2是锐角三角形 |
| D.△A1B1C1是锐角三角形,△A2B2C2是钝角三角形 |
用反证法证明“自然数a,b,c中恰有一个偶数”时,下列假设正确的是 ( )
| A.假设a,b,c都是奇数或至少有两个偶数 |
| B.假设a,b,c都是偶数 |
| C.假设a,b,c至少有两个偶数 |
| D.假设a, b,c都是奇数 |
用反证法证明命题:“三角形的内角中至少有一个不大于60度”时,反设正确的是( )
| A.假设三内角都大于60度; |
| B.假设三内角都不大于60度; |
| C.假设三内角至多有一个大于60度; |
| D.假设三内角至多有两个大于60度。 |
菱形的对角线相等,正方形是菱形,所以正方形的对角线相等。在以上三段论的推理中( )
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.结论错误 |
已知集合A={3m+2n|m>n且m,n∈N},若将集合A中的数按从小到大排成数列{an},则有a1=31+2×0=3,a2=32+2×0=9,a3=32+2×1=11,a4=33=27,…,依此类推,将数列依次排成如图所示的三角形数阵,则第六行第三个数为( )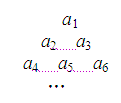
| A.247 | B.735 |
| C.733 | D.731 |
下面四个判断中,正确的是( )
| A.式子1+k+k2+…+kn(n∈N*)中,当n=1时式子值为1 |
| B.式子1+k+k2+…+kn-1(n∈N*)中,当n=1时式子值为1+k |
C.式子1+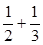 +…+ +…+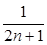 (n∈N*)中,当n=1时式子值为1+ (n∈N*)中,当n=1时式子值为1+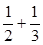 |
D.设f(x)=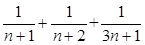 (n∈N*),则f(k+1)=f(k)+ (n∈N*),则f(k+1)=f(k)+ |
由“正三角形的内切圆切于三边的中点”可类比猜想:正四面体的内切球切于四个面( )
| A.各正三角形内一点 | B.各正三角形的某高线上的点 |
| C.各正三角形的中心 | D.各正三角形外的某点 |
观察下列各式:a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…,则a8+b8=( )
| A.28 | B.47 | C.76 | D.123 |
 ,定义运算
,定义运算 ,其中
,其中 是常数,等式右边的运算是通常的加法和乘法运算。已知
是常数,等式右边的运算是通常的加法和乘法运算。已知 ,并且有一个非零常数
,并且有一个非零常数 ,使得对任意实数
,使得对任意实数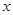 , 都有
, 都有 ,则
,则


