题目内容
用反证法证明命题:“三角形的内角中至少有一个不大于60度”时,反设正确的是( )
| A.假设三内角都大于60度; |
| B.假设三内角都不大于60度; |
| C.假设三内角至多有一个大于60度; |
| D.假设三内角至多有两个大于60度。 |
A
解析试题分析:根据反证法的步骤,假设是对原命题结论的否定,“至少有一个”的否定:“一个也没有”;即“三内角都大于60度”.故选B.
考点:反证法与放缩法.

练习册系列答案
相关题目
如图所示的三角形数组是我国古代数学家杨辉发现的,称为杨辉三角形,根据图中的数构成的规律, 所表示的数是
所表示的数是
| A.2 | B.4 | C.6 | D.8 |
用反证法证明命题:“若
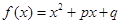 ,那么
,那么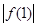 ,
,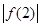 ,
,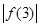 中至少有一个不小于
中至少有一个不小于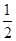 ”时,反设正确的是( )
”时,反设正确的是( )
A.假设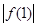 , ,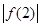 , ,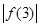 至多有两个小于 至多有两个小于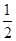 |
B.假设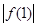 , ,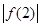 , ,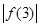 至多有一个小于 至多有一个小于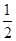 |
C.假设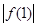 , ,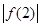 , ,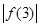 都不小于 都不小于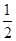 |
D.假设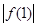 , ,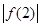 , ,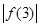 都小于 都小于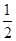 |
观察下列各式:a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…,则a8+b8=( )
| A.28 | B.47 | C.76 | D.123 |
观察下列等式,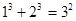 ,
,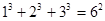 ,
,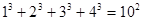 根据上述规律,
根据上述规律,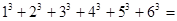 ( )
( )
A.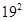 | B.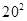 | C.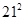 | D.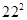 |
(推理)三角形的内角和为180º,凸四边形内角和为360º,那么凸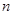 边形的内角和为
边形的内角和为
A.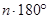 | B.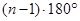 | C.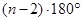 | D.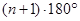 |
下列几种推理过程是演绎推理的是( )
| A.某校高三1班55人,2班54人,3班52人,由此得高三所有班级的人数超过50人 |
| B.由圆的周长C=πd推测球的表面积S=πd2 |
| C.两条直线平行,同旁内角互补,如果∠A与∠B是两条平行直线的同旁内角,则∠A+∠B=180° |
D.在数列{an}中,a1=1,an=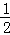 (an﹣1+ (an﹣1+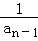 )(n≥2),由此归纳数列{an}的通项公式 )(n≥2),由此归纳数列{an}的通项公式 |
由集合{a1},{a1,a2},{a1,a2,a3},…的子集个数归纳出集合{a1,
a2,a3,…,an}的子集个数为( )
| A.n | B.n+1 |
| C.2n | D.2n-1 |
 、
、 、
、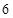 、
、 、
、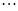 按表
按表 的方式进行排列,记
的方式进行排列,记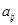 表示第
表示第 行和第
行和第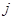 列的数,若
列的数,若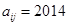 ,则
,则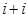 的值为( )
的值为( ) 列
列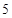 列
列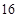
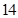

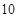
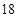

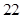
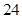
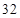

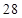
 B.
B. C.
C. D.
D.