题目内容
用反证法证明命题:“三角形的内角中至少有一个不大于60度”时,假设正确的是( )
| A．假设三个内角都不大于60度 |
| B．假设三个内角都大于60度 |
| C．假设三个内角至多有一个大于60度 |
| D．假设三个内角有两个大于60度 |
B
解析
练习册系列答案
相关题目
菱形的对角线相等，正方形是菱形，所以正方形的对角线相等。在以上三段论的推理中（ ）
| A．大前提错误 | B．小前提错误 | C．推理形式错误 | D．结论错误 |
已知数列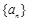
的前
项和为
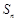，且
，
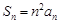
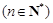，可归纳猜想出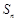的表达式为( )
A． | B． | C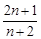． | D． |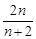
用反证法证明命题：“一个三角形中不能有两个直角”的过程归纳为以下三个步骤：
①
，这与三角形内角和为
相矛盾，
不成立；②所以一个三角形中不能有两个直角；③假设三角形的三个内角
、
、
中有两个直角，不妨设，正确顺序的序号为
| A．①②③ | B．③①② | C．①③② | D．②③① |
某个命题与自然数n有关，若n＝k(k∈N*)时命题成立，那么可推得当n＝k＋1时该命题也成立，现已知n＝5时，该命题不成立，那么可以推得( )
| A．n＝6时该命题不成立 | B．n＝6时该命题成立 |
| C．n＝4时该命题不成立 | D．n＝4时该命题成立 |
圆周上2个点可连成1条弦,这条弦可将圆面划分成2部分;圆周上3个点可连成3条弦,这3条弦可将圆面划分成4部分;圆周上4个点可连成6条弦,这6条弦最多可将圆面划分成8部分.则这些弦最多可把圆面分成 ( ) 部分
| A．2n-1 | B．2n | C．2n+1 | D．2n+2 |
观察下列各式：72=49，73=343，74=2401，…，则72011的末两位数字为（ ）
| A．01 | B．43 | C．07 | D．49 |
用数学归纳法证明“n3＋(n＋1)3＋(n＋2)3，(n∈N＋)能被9整除”，要利
用归纳法假设证n＝k＋1时的情况，只需展开( )．
| A．(k＋3)3 | B．(k＋2)3 |
| C．(k＋1)3 | D．(k＋1)3＋(k＋2)3 |
在用数学归纳法证明凸n边形内角和定理时,第一步应验证( )
| A．n=1时成立 | B．n=2时成立 |
| C．n=3时成立 | D．n=4时成立 |