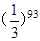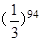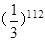题目内容
已知集合A={3m+2n|m>n且m,n∈N},若将集合A中的数按从小到大排成数列{an},则有a1=31+2×0=3,a2=32+2×0=9,a3=32+2×1=11,a4=33=27,…,依此类推,将数列依次排成如图所示的三角形数阵,则第六行第三个数为( )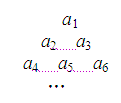
| A.247 | B.735 |
| C.733 | D.731 |
C
解析试题分析:该三角形数阵中,每一行所排的数成等差数列,首项为1,公差为1,
因此前5行已经排了 ×5=15个数,
×5=15个数,
∴第六行第三个数是数列中的第18项,
∵a1=31+2×0=3,a2=32+2×0=9,a3=32+2×1=11,a4=33=27,…
∴a18=36+2×2=733,
故选C.
考点:进行简单的合情推理.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
用火柴棒摆“金鱼”,如图所示: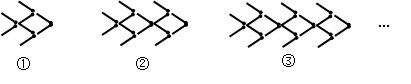
按照上面的规律,第4个“金鱼”图需要火柴棒的根数为
| A.24 | B.26 | C.28 | D.30 |
用数学归纳法证明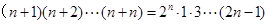 (
(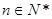 )时,从“
)时,从“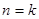 到
到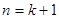 ”左边需增乘的代数式为( )
”左边需增乘的代数式为( )
A.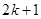 | B.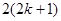 | C.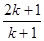 | D. |
下列表述正确的是
①归纳推理是由部分到整体的推理;②归纳推理是由一般到一般的推理;③演绎推理是由一般到特殊的推理;④类比推理是由特殊到一般的推理;⑤类比推理是由特殊到特殊的推理.
| A.①②③ | B.②③④ | C.②④⑤ | D.①③⑤ |
观察下列各式:a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…,则a10+b10=( )
| A.28 | B.76 | C.123 | D.199 |
如果△A1B1C1的三个内角的余弦值分别等于△A2B2C2的三个内角的正弦值,那么( )
| A.△A1B1C1和△A2B2C2都是锐角三角形 |
| B.△A1B1C1和△A2B2C2都是钝角三角形 |
| C.△A1B1C1是钝角三角形,△A2B2C2是锐角三角形 |
| D.△A1B1C1是锐角三角形,△A2B2C2是钝角三角形 |
下面几种推理过程是演绎推理的是( )
| A.某校高三有8个班,1班有51人,2班有53人,3班有52人,由此推测各班人数都超过50人 |
| B.由三角形的性质,推测空间四面体的性质 |
| C.平行四边形的对角线互相平分,菱形是平行四边形,所以菱形的对角线互相平分 |
D.在数列{an}中,a1=1,an=  ,由此归纳出{an}的通项公式 ,由此归纳出{an}的通项公式 |
 、
、 、
、 、
、 、
、 按表
按表 的方式进行排列,记
的方式进行排列,记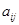 表示第
表示第 行和第
行和第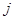 列的数,若
列的数,若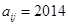 ,则
,则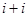 的值为( )
的值为( ) 列
列 列
列




 B.
B. C.
C. D.
D.
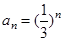 ,把数列
,把数列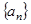 的各项排列成如下的三角形状,
的各项排列成如下的三角形状,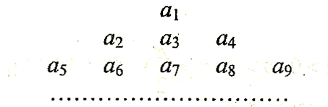
 表示第
表示第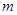 行的第
行的第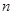 个数,则
个数,则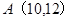 = ( )
= ( )