仔细观察下面○和●的排列规律:
○●○○●○○○●○○○○●○○○○○●○○○○○○ ●……
若依此规律继续下去,得到一系列的○和●,那么在前120个○和●中,●的个数是( )
| A.13 | B.14 | C.15 | D.16 |
用反证法证明命题:“若
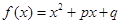 ,那么
,那么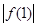 ,
,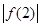 ,
,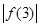 中至少有一个不小于
中至少有一个不小于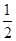 ”时,反设正确的是( )
”时,反设正确的是( )
A.假设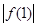 , ,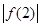 , ,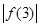 至多有两个小于 至多有两个小于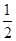 |
B.假设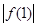 , ,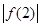 , ,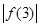 至多有一个小于 至多有一个小于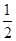 |
C.假设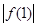 , ,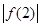 , ,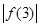 都不小于 都不小于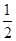 |
D.假设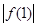 , ,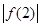 , ,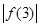 都小于 都小于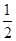 |
要证明 ,可选择的方法有以下几种,其中最合理的是( )
,可选择的方法有以下几种,其中最合理的是( )
| A.综合法 | B.分析法 | C.反证法 | D.归纳法 |
用数学归纳法证明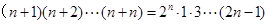 (
(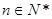 )时,从“
)时,从“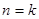 到
到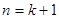 ”左边需增乘的代数式为( )
”左边需增乘的代数式为( )
A.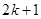 | B.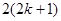 | C.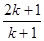 | D. |
下面几种推理中是演绎推理的序号为( )
A.半径为 圆的面积 圆的面积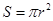 ,则单位圆的面积 ,则单位圆的面积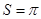 ; ; |
| B.由金、银、铜、铁可导电,猜想:金属都可导电; |
| C.由平面三角形的性质,推测空间四面体性质; |
D.由平面直角坐标系中圆的方程为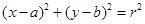 ,推测空间直角坐标系中球的方程为 ,推测空间直角坐标系中球的方程为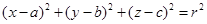 . . |
用反证法证明命题:“若a,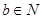 ,
,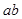 能被5整除,则a,b中至少有一个能被5整除”,那么假设的内容是( )
能被5整除,则a,b中至少有一个能被5整除”,那么假设的内容是( )
| A.a,b都能被5整除 | B.a,b都不能被5整除 |
| C.a,b有一个能被5整除 | D.a,b有一个不能被5整除 |
已知数列2,5,11,20,x,47, 合情推出x的值为( )
| A.29 | B.31 | C.32 | D.33 |
利用数学归纳法证明不等式1+ +
+ +
+  <f(n) (n≥2,
<f(n) (n≥2, )的过程中,由n=k变到n=k+1时,左边增加了( )
)的过程中,由n=k变到n=k+1时,左边增加了( )
| A.1项 | B.k项 | C. 项 项 | D. 项 项 |
 、
、 、
、 、
、 号位上(如图),第一次前后
号位上(如图),第一次前后 这样交替进行下去,那么第
这样交替进行下去,那么第 次互换座位后,小兔坐
次互换座位后,小兔坐