题目内容
要证明 ,可选择的方法有以下几种,其中最合理的是( )
,可选择的方法有以下几种,其中最合理的是( )
| A.综合法 | B.分析法 | C.反证法 | D.归纳法 |
B
解析试题分析:因为条件没有,直接证明比较难以说明,只要分析法,要证明结论,转换为有理式,需要将两边平方法,这样就可以借助于我们有理数的大小关系来判定了,故选B.
考点:不等式的证明方法——分析法.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
下列正确的是( )
| A.类比推理是由特殊到一般的推理 |
| B.演绎推理是由特殊到一般的推理 |
| C.归纳推理是由个别到一般的推理 |
| D.合情推理可以作为证明的步骤 |
用演绎法证明函数 是增函数时的小前提是
是增函数时的小前提是
| A.增函数的定义 |
B.函数 满足增函数的定义 满足增函数的定义 |
C.若 ,则 ,则 |
D.若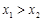 ,则 ,则 |
利用数学归纳法证明不等式1+ +
+ +
+  <f(n) (n≥2,
<f(n) (n≥2, )的过程中,由n=k变到n=k+1时,左边增加了( )
)的过程中,由n=k变到n=k+1时,左边增加了( )
| A.1项 | B.k项 | C. 项 项 | D. 项 项 |
如图,第n个图形是由正n+2边形“扩展”而来,(n=1、2、3、…),
则在第n个图形中共有( )个顶点。
| A.(n+1)(n+2) | B.(n+2)(n+3) | C. +3n+8 +3n+8 | D.12n |
菱形的对角线相等,正方形是菱形,所以正方形的对角线相等。在以上三段论的推理中( )
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.结论错误 |
四个小动物换座位,开始是猴、兔、猫、鼠分别坐在1、2、3、4号位置上(如图),第1次前后排动物互换位置,第2次左右列互换座位,……这样交替进行下去,那么第2014次互换座位后,小兔的位置对应的是( )
| A.编号1 | B.编号2 | C.编号3 | D.编号4 |
圆周上2个点可连成1条弦,这条弦可将圆面划分成2部分;圆周上3个点可连成3条弦,这3条弦可将圆面划分成4部分;圆周上4个点可连成6条弦,这6条弦最多可将圆面划分成8部分.则这些弦最多可把圆面分成 ( ) 部分
| A.2n-1 | B.2n | C.2n+1 | D.2n+2 |
如图,模块①~⑤均由4个棱长为1的小正方体构成,模块⑥由15个棱长为1的小正方体构成.现从模块①~⑤中选出三个放到模块⑥上,使得模块⑥成为一个棱长为3的大正方体,则下列选择方案中,能够完成任务的为( )
| A.模块①,②,⑤ | B.模块①,③,⑤ |
| C.模块②,④,⑤ | D.模块③,④,⑤ |