题目内容
10.已知cotα=-2,求$\frac{4sinα-2cosα}{4cosα+3sinα}$的值.分析 由已知及同角三角函数基本关系式可求tanα=-$\frac{1}{2}$,利用同角三角函数基本关系式化简所求后代入计算即可得解.
解答 解:∵cotα=-2,可得:tanα=-$\frac{1}{2}$,
∴$\frac{4sinα-2cosα}{4cosα+3sinα}$=$\frac{4tanα-2}{4+3tanα}$=$\frac{4×(-\frac{1}{2})-2}{4+3×(-\frac{1}{2})}$=-$\frac{8}{5}$.
点评 本题主要考查了同角三角函数基本关系式在三角函数化简求值中的应用,考查了转化思想,属于基础题.

练习册系列答案
相关题目
20.过点M(2,-1)作斜率为$\frac{1}{2}$的直线与椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)相交于A,B两个不同点,若M是AB的中点,则该椭圆的离心率e=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{3}{4}$ |
5.若tanα=-2,则sinα=( )
| A. | $\frac{2\sqrt{5}}{5}$ | B. | -$\frac{2\sqrt{5}}{5}$ | C. | ±$\frac{\sqrt{5}}{5}$ | D. | ±$\frac{2\sqrt{5}}{5}$ |
16.命题“?x∈R,f(x)<g(x)<h(x)”的否定形式是( )
| A. | ?x0∈R,f(x0)≥g(x0)≥h(x0) | B. | ?x0∈R,f(x0)≥g(x0)或g(x0)≥h(x0) | ||
| C. | ?x∈R,f(x)≥g(x)≥h(x) | D. | ?x∈R,f(x)≥g(x)或g(x)≥h(x) |
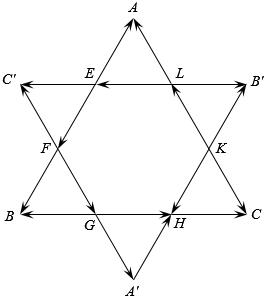 如图所示,△ABC和△A′B′C′是在各边的$\frac{1}{3}$处相交的两个全等的正三角形,设△ABC的边长为a,图中列出了长度均为$\frac{a}{3}$的若干个向量,求:
如图所示,△ABC和△A′B′C′是在各边的$\frac{1}{3}$处相交的两个全等的正三角形,设△ABC的边长为a,图中列出了长度均为$\frac{a}{3}$的若干个向量,求: