题目内容
2．若函数y=x3+x2+mx+1在[0，1]上的单调递增，则m的取值范围是[0，+∞）．分析 对函数进行求导，令导函数大于等于0在（0，1）上恒成立即可．
解答 解：若函数y=x3+x2+mx+1在（0，1）上得到递增，
只需y′=3x2+2x+m≥0在（0，1）恒成立，
即m≥-3x2-2x在（0，1）恒成立即可，
令f（x）=-3x2-2x，对称轴x=-$\frac{1}{3}$，
∴f（x）在（0，1）递减，
∴f（x）max=f（0）=0，
∴只需m≥f（x）max=0，
故答案为：[0，+∞）．
点评 题主要考查函数的单调性与其导函数的正负之间的关系．即当导数大于0是原函数单调递增，当导数小于0时原函数单调递减．
练习册系列答案
相关题目
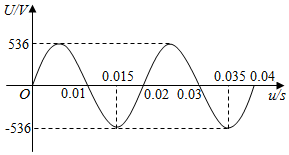一台发电机产生地交流电的电压U和时间t之间关系的图象如图所示，由图象说出它的周期、频率和电压的最大值，并求出电压U和时间t之间的函数解析式．
设a∈R，f（x）=cosx（asinx-cosx）+cos2$（{\frac{π}{2}-x}）$满足f $（{-\frac{π}{3}}）$=f（0），