题目内容
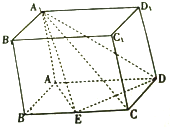 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,且AB=1,BC=2,∠ABC=60°,E为BC的中点,AA1⊥平面ABCD.
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,且AB=1,BC=2,∠ABC=60°,E为BC的中点,AA1⊥平面ABCD.(1)求证:B1C∥平面A1DE;
(2)求证:平面A1AE⊥平面A1DE.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)连结B1C,由已知得B1C∥A1D,由此能证明B1C∥平面A1DE.
(2)由题意得△ABE是正三角形,∠AEB=60°,∠CED=∠CDE=
(180°-∠ECD)=30°,从而DE⊥AE,进而DE⊥平面A1AE,由此能证明平面A1AE⊥平面A1DE.
(2)由题意得△ABE是正三角形,∠AEB=60°,∠CED=∠CDE=
| 1 |
| 2 |
解答:
证明:(1)连结B1C,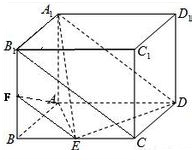
∵四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,
∴B1C∥A1D,
又B1C?平面A1DE,A1D?平面A1DE,
∴B1C∥平面A1DE.
(2)由题意得BE=EC=
BC=AB=CD,
∴△ABE是正三角形,∠AEB=60°,
又△CDE中,∠CED=∠CDE=
(180°-∠ECD)=30°,
∴∠AED=180°-∠CED-∠AEB=90°,即DE⊥AE,
∵AA1∩AE=A,∴DE⊥平面A1AE,
∵DE?平面A1DE,∴平面A1AE⊥平面A1DE.

∵四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,
∴B1C∥A1D,
又B1C?平面A1DE,A1D?平面A1DE,
∴B1C∥平面A1DE.
(2)由题意得BE=EC=
| 1 |
| 2 |
∴△ABE是正三角形,∠AEB=60°,
又△CDE中,∠CED=∠CDE=
| 1 |
| 2 |
∴∠AED=180°-∠CED-∠AEB=90°,即DE⊥AE,
∵AA1∩AE=A,∴DE⊥平面A1AE,
∵DE?平面A1DE,∴平面A1AE⊥平面A1DE.
点评:本题考查线面平行、面面垂直的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
在区间[-
,
]上随机取一个数x,则cosπx的值介于
与
之间的概率为( )
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知i是虚数单位,m和n都是实数,且m(1+i)=
+m,则(
)2015=( )
| 3 |
| m+ni |
| m-ni |
| A、-1 | B、1 | C、-i | D、i |
已知集合P={x|x2-1≤0},M={a},若P∪M=P,则实数a的取值范围是( )
| A、(-∞,-1] |
| B、[1,+∞) |
| C、[-1,1] |
| D、(-∞,-1]∪[1,+∞) |
z=
(i是虚数单位)则z的共轭复数为( )
| 5i |
| 1-2i |
| A、2-i | B、2+i |
| C、-2-i | D、-2+i |
已知集合A={x|0<x<2},B={x||x|>1},则A∩B=( )
| A、(0,1) |
| B、(1,2) |
| C、(-∞,-1)∪(0,+∞) |
| D、(-∞,-1)∪(1,+∞) |