题目内容
已知集合P={x|x2-1≤0}，M={a}，若P∪M=P，则实数a的取值范围是（ ）
| A、（-∞，-1] |
| B、[1，+∞） |
| C、[-1，1] |
| D、（-∞，-1]∪[1，+∞） |
考点：并集及其运算
专题：集合
分析：化简集合P，若P∪M=P，可得M⊆P，由此求得实数a的取值范围，
解答：
解：∵集合P={x|x2-1≤0}={x|-1≤x≤1}=[-1，1]，M={a}，P∪M=P，
∴M⊆P，
∴a∈[-1，1]，
故选：C
∴M⊆P，
∴a∈[-1，1]，
故选：C
点评：本题主要考查集合中参数的取值问题，两个集合的并集的定义，判断 M⊆P是解题的关键，属于基础题
练习册系列答案
相关题目
函数f（x）=2x-tanx在（-
，
）上的图象大致是（ ）
| π |
| 2 |
| π |
| 2 |
A、 |
B、 |
C、 |
D、 |
实数x，y满足
，若t≤y+2x恒成立，则t的取值范围是（ ）
|
| A、t≤13 | B、t≤-5 |
| C、t≤-13 | D、t≤5 |
设全集U={0，1，2，3，4}，集合A={0，1，2}，集合b={2，3}，则（∁UA）∪B=（ ）
| A、∅ |
| B、{1，2，3，4} |
| C、{2，3，4} |
| D、{0，11，2，3，4} |
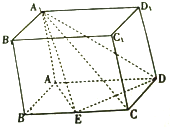如图，四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形，且AB=1，BC=2，∠ABC=60°，E为BC的中点，AA1⊥平面ABCD．复数z=
+ai（a∈R且a≠0）对应的点在复平面内位于（ ）
| 1 |
| a |
| A、第一、二象限 |
| B、第一、三象限 |
| C、第二、四象限 |
| D、第三、四象限 |