题目内容
已知圆C:(x-2)2+y2=2,若直线l与圆C相切,且在两坐标轴上的截距相等,求直线l的方程.
考点:圆的切线方程
专题:直线与圆
分析:当直线过原点时斜率存在,设方程为y=kx,当直线不过原点时,设直线的方程为
+
=1,分别联立方程由△=0可得.
| x |
| a |
| y |
| a |
解答:
解:当直线过原点时斜率存在,设方程为y=kx,
联立
消去y可得(k2+1)x2-4x+2=0,
由相切可得△=16-8(k2+1)=0,解得k=±1,
∴所求直线的方程为y=±x,即x±y=0;
当直线不过原点时,设直线的方程为
+
=1,即y=a-x,
联立
消去y可得2x2-(4+2a)x+a2+3=0,
由相切可得△=(4+2a)2-8(a2+3)=0,解得a=2±
,
∴所求直线的方程为x+y-(2±
)=0
综上可得所求直线的方程为:x±y=0或x+y-(2±
)=0
联立
|
由相切可得△=16-8(k2+1)=0,解得k=±1,
∴所求直线的方程为y=±x,即x±y=0;
当直线不过原点时,设直线的方程为
| x |
| a |
| y |
| a |
联立
|
由相切可得△=(4+2a)2-8(a2+3)=0,解得a=2±
| 2 |
∴所求直线的方程为x+y-(2±
| 2 |
综上可得所求直线的方程为:x±y=0或x+y-(2±
| 2 |
点评:本题考查直线与圆的相切关系,涉及分类讨论的思想和一元二次方程的根与判别式的关系,属中档题.

练习册系列答案
相关题目
若某空间几何体的三视图如图所示,则该几何体的体积是( )


| A、3 | B、4 | C、6 | D、12 |
函数f(x)=logax+x-b(2<a<3<b<4)的零点所在的一个区间是( )
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
函数f(x)的图象如图所示,则f(x)的解析式可能是( )


| A、f(x)=2lnx+x-1 | ||
| B、f(x)=2lnx-x+1 | ||
| C、f(x)=2xlnx | ||
D、f(x)=
|
下列命题中的假命题是( )
| A、?x∈R,lgx=0 |
| B、?x∈R,tanx=2 |
| C、?x∈R,x2≥0 |
| D、?x∈R,2 x2+2x>1 |
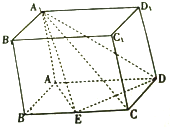 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,且AB=1,BC=2,∠ABC=60°,E为BC的中点,AA1⊥平面ABCD.
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,且AB=1,BC=2,∠ABC=60°,E为BC的中点,AA1⊥平面ABCD.
 在△ABC中,A的外角平分线交BC的延长线于D,已知AB:AC=2:1,求BD:DC.
在△ABC中,A的外角平分线交BC的延长线于D,已知AB:AC=2:1,求BD:DC.