题目内容
每年暑假期间,安徽卫视播出的《男生女生向前冲》闯关节目都非常火,闯关规则为:如果单人通过所有关卡达到终点,则可获得一台空调,今年高考结束够,高三某班学生为了放松一下,挑选了3名男生.3名女生组成男生队与女生队两个队伍参加这档节目,3名男生能成功到达终点得概率分别为
,
,
.3名女生体质差不多,每位女生能成功到达终点得概率均为
(男生和女生之间没有影响)
(1)求男生队没有获得空调且女生队获得三台空调的概率;
(2)设男生队获得空调的台数为ξ,求ξ的分布列与数学期望.
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 5 |
(1)求男生队没有获得空调且女生队获得三台空调的概率;
(2)设男生队获得空调的台数为ξ,求ξ的分布列与数学期望.
考点:离散型随机变量的期望与方差,列举法计算基本事件数及事件发生的概率,离散型随机变量及其分布列
专题:概率与统计
分析:(1)男生队没有获得空调且女生队获得三台空调,是指三名男生都没有到达终点,三名女生都成功到达终点,由此能求出男生队没有获得空调且女生队获得三台空调的概率.
(2)由已知得ξ的可能取值为0,1,2,3,分别求出相应的概率,由此能求出ξ的分布列与数学期望.
(2)由已知得ξ的可能取值为0,1,2,3,分别求出相应的概率,由此能求出ξ的分布列与数学期望.
解答:
解:(1)∵男生队没有获得空调且女生队获得三台空调,
∴三名男生都没有到达终点,三名女生都成功到达终点,
∴男生队没有获得空调且女生队获得三台空调的概率:
p=(1-
)(1-
)(1-
)×(
)3=
.
(2)由已知得ξ的可能取值为0,1,2,3,
P(ξ=0)=(1-
)(1-
)(1-
)=
,
P(ξ=1)=
(1-
)(1-
)+
(1-
)(1-
)+
(1-
)(1-
)=
,
P(ξ=2)=
×
(1-
)+
(1-
)×
+(1-
)×
×
=
,
P(ξ=3)=
×
×
=
,
∴ξ的分布列为:
Eξ=0×
+1×
+2×
+3×
=
.
∴三名男生都没有到达终点,三名女生都成功到达终点,
∴男生队没有获得空调且女生队获得三台空调的概率:
p=(1-
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 5 |
| 1 |
| 250 |
(2)由已知得ξ的可能取值为0,1,2,3,
P(ξ=0)=(1-
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 2 |
P(ξ=1)=
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 4 |
| 1 |
| 5 |
| 47 |
| 120 |
P(ξ=2)=
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 10 |
P(ξ=3)=
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 120 |
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 1 |
| 2 |
| 47 |
| 120 |
| 1 |
| 10 |
| 1 |
| 120 |
| 37 |
| 60 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要注意对立事件概率计算公式的合理运用.

练习册系列答案
相关题目
设i是虚数单位,若复数
为纯虚数,则实数m的值为( )
| 2-mi |
| 1+i |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
已知焦点在x轴上的椭圆方程为
+
=1,随着a的增大该椭圆的形状( )
| x2 |
| 4a |
| y2 |
| a2-1 |
| A、越接近于圆 |
| B、越扁 |
| C、先接近于圆后越扁 |
| D、先越扁后接近于圆 |
设f(x)是定义在R上的偶函数,对x∈R,都有f(x-2)=f(x+2),且当x∈[-2,0]时,f(x)=(
)x-1,则函数y=f(x)-log2(x+2)的零点个数为( )
| 1 |
| 2 |
| A、7 | B、6 | C、5 | D、4 |
若某空间几何体的三视图如图所示,则该几何体的体积是( )


| A、3 | B、4 | C、6 | D、12 |
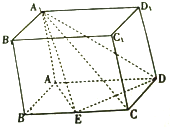 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,且AB=1,BC=2,∠ABC=60°,E为BC的中点,AA1⊥平面ABCD.
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,且AB=1,BC=2,∠ABC=60°,E为BC的中点,AA1⊥平面ABCD.
 在△ABC中,A的外角平分线交BC的延长线于D,已知AB:AC=2:1,求BD:DC.
在△ABC中,A的外角平分线交BC的延长线于D,已知AB:AC=2:1,求BD:DC.