题目内容
5.已知Sn是等比数列{an}(n∈N*)的前n项和,若S3=14,公比 q=2,则数列{an}的通项公式an=2n(N*).分析 根据等比数列的前n项和公式和通项公式求解即可.
解答 解:∵Sn是等比数列{an}(n∈N*)的前n项和,若S3=14,公比 q=2,
∴${s}_{3}=\frac{{a}_{1}(1-{2}^{3})}{1-2}=14$,
解得:a1=2,
∴${a}_{n}={2}^{n}(n∈$N*).
故答案为:2n(N*).
点评 本题主要考查等比数列的通项公式以及前n项和公式,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.已知函数f(x)=x3-3x-1,g(x)=2x-a,若对任意x1∈[0,2],存在x2∈[0,2]使|f(x1)-g(x2)|≤2,则实数a的取值范围( )
| A. | [1,5] | B. | [2,5] | C. | [-2,2] | D. | [5,9] |
20.已知命题p1:函数y=ex-e-x在R上为增函数;命题p2:函数y=ex+e-x在R上为减函数,则在命题q1:p1∨p2,q2:p1∧p2,q3:(¬p1)∨p2,q4:p1∧(¬p2)中,真命题是( )
| A. | q1、q3 | B. | q2、q3 | C. | q1、q4 | D. | q2、q4 |
10.i为虚数单位,z=$\frac{5i}{1+2i}$,则|$\overline{z}$|=( )
| A. | $\sqrt{5}$ | B. | 5 | C. | 1 | D. | 2 |
17.已知菱形ABCD的边长为2,∠BAD=120°,点E、F分别在边BC、CD上,$\overrightarrow{BE}$=λ$\overrightarrow{BC}$,$\overrightarrow{DF}$=μ$\overrightarrow{DC}$.若λ+μ=$\frac{2}{3}$,则$\overrightarrow{AE}$•$\overrightarrow{AF}$的最小值( )
| A. | $\frac{4}{9}$ | B. | $\frac{5}{9}$ | C. | $\frac{10}{9}$ | D. | $\frac{11}{9}$ |
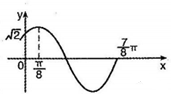 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则此函数的解析式为f(x)=2sin(2x+$\frac{π}{4}$).
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则此函数的解析式为f(x)=2sin(2x+$\frac{π}{4}$). 如图,在平面四边形ABCD中,已知E,F,G,H分别是棱AB,BC,CD,DA的中点.若|EG|2-|HF|2=1,设|AD|=x,|BC|=y,|AB|=z,|CD|=1,则$\frac{2x+y}{{z}^{2}+8}$的最大值是$\frac{1}{2}$.
如图,在平面四边形ABCD中,已知E,F,G,H分别是棱AB,BC,CD,DA的中点.若|EG|2-|HF|2=1,设|AD|=x,|BC|=y,|AB|=z,|CD|=1,则$\frac{2x+y}{{z}^{2}+8}$的最大值是$\frac{1}{2}$.