题目内容
15. 如图,在平面四边形ABCD中,已知E,F,G,H分别是棱AB,BC,CD,DA的中点.若|EG|2-|HF|2=1,设|AD|=x,|BC|=y,|AB|=z,|CD|=1,则$\frac{2x+y}{{z}^{2}+8}$的最大值是$\frac{1}{2}$.
如图,在平面四边形ABCD中,已知E,F,G,H分别是棱AB,BC,CD,DA的中点.若|EG|2-|HF|2=1,设|AD|=x,|BC|=y,|AB|=z,|CD|=1,则$\frac{2x+y}{{z}^{2}+8}$的最大值是$\frac{1}{2}$.
分析 利用平行四边形的对角线的平方和等于四条边的平方和,得出z2+3=x2+y2,$\frac{2x+y}{{z}^{2}+8}$=$\frac{2x+y}{{x}^{2}+{y}^{2}+5}$=$\frac{1}{t}$,化简配方,即可求$\frac{2x+y}{{z}^{2}+8}$的最大值.
解答 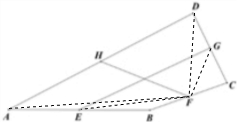 解:如图所示,连接FD,FA,FE,FG,则
解:如图所示,连接FD,FA,FE,FG,则
x2+4|HF|2=2(|AF|2+|DF|2)①
z2+4|EF|2=2(|AF|2+$\frac{1}{4}$y2)②
12+4|GF|2=2(|DF|2+$\frac{1}{4}$y2)③
②+③:z2+1+2(2|EF|2+2|GF|2)=2(|AF|2+|DF|2)+y2,
①代入z2+1+2(2|EF|2+2|GF|2)=x2+4|HF|2+y2,
∵2|EF|2+2|GF|2=|EG|2+|HF|2,
∴z2+1+2(|EG|2+|HF|2)=x2+4|HF|2+y2,
∴z2+1+2(|EG|2-|HF|2)=x2+y2,
∵|EG|2-|HF|2=1,
∴z2+3=x2+y2,
∴$\frac{2x+y}{{z}^{2}+8}$=$\frac{2x+y}{{x}^{2}+{y}^{2}+5}$=$\frac{1}{t}$,
∴(x-t)2+(y-$\frac{t}{2}$)2=-5+$\frac{5}{4}$t2≥0,
∴t≥2
∴$\frac{2x+y}{{z}^{2}+8}$的最大值为$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查求$\frac{2x+y}{{z}^{2}+8}$的最大值,考查学生分析解决问题的能力,利用平行四边形的对角线的平方和等于四条边的平方和,得出z2+3=x2+y2是关键.

| A. | 58 | B. | 59 | C. | 78 | D. | 28 |
| A. | -2$\sqrt{5}$ | B. | 2 | C. | 2$\sqrt{5}$ | D. | 1 |