题目内容
8.在一次赠书活动中,将2本不同的小说与2本不同的诗集赠给2名学生,每名学生2本书,则每人分别得到1本小说与1本诗集的概率为( )| A. | $\frac{1}{5}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{2}{3}$ |
分析 先求出基本事件总数n=${C}_{4}^{2}{C}_{2}^{2}$=6,再求出每人分别得到1本小说与1本诗集包含的基本事件个数m=($\frac{{C}_{2}^{1}{C}_{1}^{1}}{{A}_{2}^{2}}•\frac{{C}_{2}^{1}{C}_{1}^{1}}{{A}_{2}^{2}}$)×${A}_{2}^{2}$=4,由此能示出每人分别得到1本小说与1本诗集的概率.
解答 解:在一次赠书活动中,将2本不同的小说与2本不同的诗集赠给2名学生,每名学生2本书,
基本事件总数n=${C}_{4}^{2}{C}_{2}^{2}$=6,
每人分别得到1本小说与1本诗集包含的基本事件个数m=($\frac{{C}_{2}^{1}{C}_{1}^{1}}{{A}_{2}^{2}}•\frac{{C}_{2}^{1}{C}_{1}^{1}}{{A}_{2}^{2}}$)×${A}_{2}^{2}$=4,
∴每人分别得到1本小说与1本诗集的概率p=$\frac{m}{n}=\frac{4}{6}=\frac{2}{3}$.
故选:D.
点评 本题考查概率的求法,涉及到古典概型、排列组合等基础知识,考查推理论证能力、运算求解能力,考查集合思想、化归与转化思想、函数与方程思想,是基础题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
13.已知函数f(x)=ax-x2-lnx存在极值,若这些极值的和大于5+ln2,则实数a的取值范围为( )
| A. | (-∞,4) | B. | (4,+∞) | C. | (-∞,2) | D. | (2,+∞) |
20.“a>1“是“$\frac{1}{a}$<1“的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 非充分非必要条件 |
5.某校在两个班进行学习方式对比试验,半年后进行了一次检测,试验班与对照班成绩统计如2×2列联表所示(单位:人).
(1)求m,n
(2)你有多大把握认为“成绩与学习方式有关系”?
参考公式及数据:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d为样本容量.
| 80及80分以上 | 80分以下 | 合计 | |
| 试验班 | 30 | 10 | 40 |
| 对照班 | 18 | m | 40 |
| 合计 | 48 | 32 | n |
(2)你有多大把握认为“成绩与学习方式有关系”?
参考公式及数据:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d为样本容量.
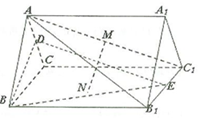 如图,正三棱柱ABC-A1B1C1中,侧棱$A{A_1}=\sqrt{3}$,AB=2,D,E分别为棱AC,B1C1的中点,M,N分别为线段AC1和BE的中点.
如图,正三棱柱ABC-A1B1C1中,侧棱$A{A_1}=\sqrt{3}$,AB=2,D,E分别为棱AC,B1C1的中点,M,N分别为线段AC1和BE的中点.