题目内容
12.在△ABC中,三个内角A,B,C所对的边分别为a,b,c,且满足$\frac{acosB+bcosA}{c}$=2cosC.(1)求角C的大小;
(2)若△ABC的面积为2$\sqrt{3}$,a+b=6,求边c的长.
分析 (1)由已知及余弦定理可得:$\frac{acosB+bcosA}{c}$=1,可求cosC=$\frac{1}{2}$,结合范围C∈(0,π)可求C的值.
(2)利用三角形面积公式可得ab=8,又a+b=6,利用余弦定理即可求值得解.
解答 解:(1)由余弦定理可得:acosB+bcosA=a×$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$+b×$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{2{c}^{2}}{2c}$=c,…3分
∴$\frac{acosB+bcosA}{c}$=1,
∴cosC=$\frac{1}{2}$,
又∵C∈(0,π),C=$\frac{π}{3}$…7分
(2)∵S△ABC=$\frac{1}{2}$absinC=2$\sqrt{3}$,∴ab=8,…10分
又∵a+b=6,
∴c2=a2+b2-2abcosC=(a+b)2-3ab=12,…13分
∴c=2$\sqrt{3}$…14分
点评 本题主要考查了余弦定理,三角形面积公式,特殊角的三角函数值的应用,属于基本知识的考查.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
17.已知动圆M与y轴相切且与定圆A:(x-3)2+y2=9外切,则动圆的圆心M的轨迹方程是( )
| A. | y2=12x(x>0) | B. | y=0(x<0) | ||
| C. | y2=12x | D. | y2=12x(x>0)或y=0(x<0) |
4.已知函数f(x)在区间[a,b]上单调,且图象是连续不断的,若f(a)•f(b)<0,则方程f(x)=0在区间[a,b]上( )
| A. | 至少有一实根 | B. | 至多有一实根 | C. | 没有实根 | D. | 必有唯一的实根 |
1.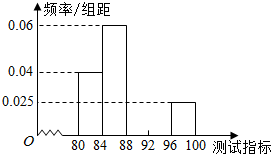 某工厂将生产的某种芯片的质量按测试指标划分为五组(指标数值越大.产品质量越好),现随机抽取芯片50件进行检测.检测结果统计如下:
某工厂将生产的某种芯片的质量按测试指标划分为五组(指标数值越大.产品质量越好),现随机抽取芯片50件进行检测.检测结果统计如下:
(1)试确定x,y,p.q的值,并补全频率分布直方图;
(2)为了挑选最优质的芯片,工厂决定在第三、四、五组中用分层抽样法抽取6件产品进行第二次检测,最终决定选用2件产品,求2件产品中至少有1件来自第四组的概率.
 某工厂将生产的某种芯片的质量按测试指标划分为五组(指标数值越大.产品质量越好),现随机抽取芯片50件进行检测.检测结果统计如下:
某工厂将生产的某种芯片的质量按测试指标划分为五组(指标数值越大.产品质量越好),现随机抽取芯片50件进行检测.检测结果统计如下:| 组号 | 测试指标 | 频数 | 频率 |
| 第一组 | [80,84] | 8 | 0.16 |
| 第二组 | [84,88] | x | 0.24 |
| 第三组 | [88,92] | 15 | p |
| 第四组 | [92,96] | 10 | q |
| 第五组 | [96,100] | y | 0.1 |
| 合 计 | 50 | 1 | |
(2)为了挑选最优质的芯片,工厂决定在第三、四、五组中用分层抽样法抽取6件产品进行第二次检测,最终决定选用2件产品,求2件产品中至少有1件来自第四组的概率.