题目内容
20.设{an}是等差数列,{bn}是各项都为正整数的等比数列,且a1=b1=1,a13b2=50,a8+b2=a3+a4+5,n∈N*.(Ⅰ)求{an},{bn}的通项公式;
(Ⅱ)设cn=(-1)n-1•λ•bn+2${\;}^{{a}_{n}}$(λ为非零实数,n为正整数),试确定实数λ的取值范围,使得对任意的正整数n,都有cn+1>cn恒成立.
分析 (Ⅰ)设{an}的公差为d,{bn}的公比为q,则依题意有q>0,利用a13b2=50,a8+b2=a3+a4+5,列出方程组,求解公差与公比,然后求解通项公式;
(Ⅱ)由cn+1>cn恒成立,讨论n的奇偶将λ进行分离,利用恒成立的方法求出λ的范围即可.
解答 解:(Ⅰ)设{an}的公差为d,{bn}的公比为q,则依题意有q>0,
且$\left\{\begin{array}{l}{(1+12d)q=50}\\{(1+7d)+q=(1+2d)+(1+3d)+5}\end{array}\right.$,
即$\left\{\begin{array}{l}{(1+12d)q=50}\\{2d+q=6}\end{array}\right.$,解得:d=q=2,或$\left\{\begin{array}{l}{d=\frac{11}{12}}\\{q=\frac{25}{6}}\end{array}\right.$,
由于{bn}是各项都为正整数的等比数列,所以d=q=2;
从而an=1+(n-1)d=2n-1,bn=qn-1=2n-1;
(Ⅱ)cn=22n-1+(-1)n-1•λ•2n-1,由cn+1>cn恒成立,
即:22n+1+(-1)n•λ•2n>22n-1+(-1)n-1•λ•2n-1,
即有2n>(-1)n-1•λ恒成立.
当n为奇数时,2n>λ,由2n递增,可得n=1时,取得最小值2,
即有λ<2;
当n为偶数时,2n>-λ,由2n递增,可得n=2时,取得最小值4,
即有-λ<4,解得λ>-4;
故实数λ的取值范围是(-4,2).
点评 本题考查等差数列和等比数列的通项公式的运用,考查数列的单调性问题的解法,注意运用分类讨论的思想方法,属于中档题.

练习册系列答案
相关题目
10.若圆C的半径为1,其圆心与点(1,0)关于直线y=x对称,则圆C的标准方程为( )
| A. | (x-1)2+y2=1 | B. | x2+(y+1)2=1 | C. | x2+(y-1)2=1 | D. | (x+1)2+y2=1 |
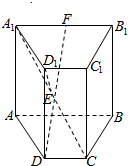 已知四棱柱ABCD-A1B1C1D1的侧棱AA1⊥底面ABCD,ABCD是等腰梯形,AB∥DC,AB=2,AD=1,∠ABC=60°,E,F分别是A1C,A1B1的中点.
已知四棱柱ABCD-A1B1C1D1的侧棱AA1⊥底面ABCD,ABCD是等腰梯形,AB∥DC,AB=2,AD=1,∠ABC=60°,E,F分别是A1C,A1B1的中点.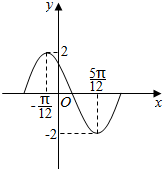 函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<π)在一个周期内的图象如图,此函数的解析式为y=2sin(2x+$\frac{2π}{3}$).
函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<π)在一个周期内的图象如图,此函数的解析式为y=2sin(2x+$\frac{2π}{3}$).