题目内容
19.若α∈(0,π),sinα+cosα=$\frac{1}{2}$,求tanα的值..分析 由已知得sinα+cosα=$\frac{1}{2}$,sinα-cosα=$\frac{\sqrt{7}}{2}$,由此能求出 tanα.
解答 解:∵α∈(0,π),sinα+cosα=$\frac{1}{2}$,①
∴两边平方得 1+2sinαcosα=$\frac{1}{4}$,∴sinαcosα=-$\frac{3}{8}$,
∵α∈(0,π),∴sinα>0,cosα<0,sinα-cosα>0,
(sinα-cosα)2=(sinα+cosα)2-4sinαcosα=$\frac{1}{4}$+$\frac{3}{2}$=$\frac{7}{4}$,
sinα-cosα=$\frac{\sqrt{7}}{2}$,②
①+②,得:2sinα=$\frac{1+\sqrt{7}}{2}$,sinα=$\frac{1+\sqrt{7}}{2}$,
①-②2cosα=$\frac{1-\sqrt{7}}{2}$,cosα=$\frac{1-\sqrt{7}}{4}$,
∴tanα=$\frac{sinα}{cosα}$=$\frac{1+\sqrt{7}}{1-\sqrt{7}}$=-$\frac{4+\sqrt{7}}{3}$.
点评 本题考查三角函数值的求法,是中档题,解题时要认真审题,注意同角三角函数关系式的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.已知正方体ABCD-A1B1C1D1,下列向量的数量积不为0的是( )
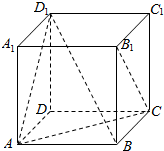

| A. | $\overrightarrow{A{D}_{1}}•\overrightarrow{{B}_{1}C}$ | B. | $\overrightarrow{B{D}_{1}}•\overrightarrow{AC}$ | C. | $\overrightarrow{B{D}_{1}}•\overrightarrow{BC}$ | D. | $\overrightarrow{AB}•\overrightarrow{A{D}_{1}}$ |
10.设i为虚数单位,则复数Z=$\frac{5+i}{1-i}$的共轭复数$\overline{Z}$为( )
| A. | 2-3i | B. | -2-3i | C. | -2+3i | D. | 2+3i |