题目内容
5.等差数列{an}中,已知a7=-8,a17=-28.(1)求数列{an}的通项公式;
(2)求Sn的最大值.
分析 (1)利用等差数列的通项公式列出方程组,求出首项和公差,由此能求出数列{an}的通项公式.
(2)由${S}_{n}=-{n}^{2}+5n$=-(n-$\frac{5}{2}$)2+$\frac{25}{4}$,能求出Sn的最大值.
解答 解:(1)设等差数列{an}中首项为a1,公差为d.
因为a7=-8,a17=-28,
所以$\left\{\begin{array}{l}{{a}_{1}+6d=-8}\\{{a}_{1}+16d=-28}\end{array}\right.$,
解得a1=4,d=-2,
所以an=a1+(n-1)d=-2n+6.
(2)由(1)可得${S}_{n}=-{n}^{2}+5n$=-(n-$\frac{5}{2}$)2+$\frac{25}{4}$,
所以当n=2或n=3时,Sn取得最大值.
(Sn)max=-22+2×5=-32+3×5=6.
点评 本题考查等差数列的通项公式的求法,考查等差数列的前n项和的最大值的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
15.要得到函数y=2sin(2x+$\frac{π}{5}$)的图象,应该把函数y=cos(x-$\frac{2}{15}$π)-$\sqrt{3}$sin(x-$\frac{2π}{15}$)的图象做如下变换( )
| A. | 将图象上的每一点横坐标缩短到原来的$\frac{1}{2}$而纵坐标不变 | |
| B. | 沿x向左平移$\frac{π}{2}$个单位,再把得图象上的每一点横坐标伸长到原来的2而纵坐标不变 | |
| C. | 先把图象上的每一点横坐标缩短到原来的$\frac{1}{2}$而纵坐标不变,再将所得图象沿x向右平移$\frac{π}{4}$个单位 | |
| D. | 先把图象上的每一点横坐标缩短到原来的$\frac{1}{2}$而纵坐标不变,再将所得图象沿x向左平移$\frac{π}{2}$个单位 |
17.已知f(x)是可导的函数,且f′(x)<f(x)对于x∈R恒成立,则( )
| A. | f(1)<ef(0),f(2017)>e2017f(0) | B. | f(1)>ef(0),f(2017)>e2017f(0) | ||
| C. | f(1)>ef(0),f(2017)<e2017f(0) | D. | f(1)<ef(0),f(2017)<e2017f(0) |
14.两人打靶,甲击中目标的概率为0.8,乙击中目标的概率为0.7,若两人同时射击一目标,则他们都击中目标的概率是( )
| A. | 0.6 | B. | 0.48 | C. | 0.75 | D. | 0.56 |
15.将直线l向左平移$\sqrt{3}$个单位,再向上平移1个单位后所得直线与l重合,则直线l的倾斜角为( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
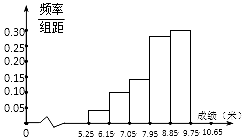 某校举行运动会,其中三级跳远的成绩在8.0米 (四舍五入,精确到0.1米) 以上的进入决赛,把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.
某校举行运动会,其中三级跳远的成绩在8.0米 (四舍五入,精确到0.1米) 以上的进入决赛,把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.