题目内容
5.知函数f(x)=ex-ax的图象在区间(-1,+∞)内与x轴没有交点,则实数a的取值范围是( )| A. | [-$\frac{1}{e}$,e) | B. | (-$\frac{1}{e}$,e) | C. | (-$\frac{1}{e}$,$\frac{1}{e}$) | D. | (0,e) |
分析 化简可得函数y=ex与y=ax的图象在区间(-1,+∞)内没有交点,从而利用数形结合的方法求解.
解答 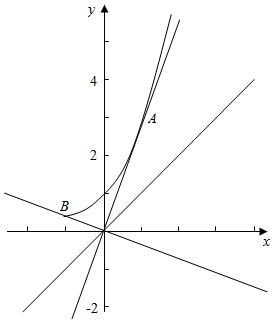 解:∵函数f(x)=ex-ax的图象在区间(-1,+∞)内与x轴没有交点,
解:∵函数f(x)=ex-ax的图象在区间(-1,+∞)内与x轴没有交点,
∴函数y=ex与y=ax的图象在区间(-1,+∞)内没有交点,
作函数y=ex与y=ax的图象在区间(-1,+∞)内的图象如右图,
当直线y=ax过点B(-1,$\frac{1}{e}$)时,a=-$\frac{1}{e}$;
当直线y=ax与y=ex相切时,设切点为A(x,ex),
故ex=$\frac{{e}^{x}}{x}$,解得,x=1;
故点A(1,e),
故a=e;
故实数a的取值范围是[-$\frac{1}{e}$,e),
故选:A.
点评 本题考查了导数的综合应用及数形结合的思想应用,同时考查了转化思想的应用,属于中档题.

练习册系列答案
相关题目
20.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x}-1,x>0}\\{-ax+1,x≤0}\end{array}\right.$,若f(a)+f(2)=0,则实数a的值等于( )
| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
10.已知函数f(x)=-x+log2$\frac{1-x}{1+x}$,若方程m-e-x=f(x)在[-$\frac{1}{3}$,$\frac{1}{3}$]内有实数解,则实数m的最小值是( )
| A. | e${\;}^{-\frac{1}{3}}$+$\frac{4}{3}$ | B. | e${\;}^{\frac{1}{3}}$+$\frac{4}{3}$ | C. | e${\;}^{\frac{1}{3}}$-$\frac{4}{3}$ | D. | e${\;}^{-\frac{1}{3}}$-$\frac{4}{3}$ |
4.已知F为双曲线$C:\frac{x^2}{9}-\frac{y^2}{16}=1$的左焦点,P,Q为C右支上的点,若PQ的长等于虚轴长的2倍,点A(5,0)在线段PQ上,则△PFQ的周长为( )
| A. | 28 | B. | 36 | C. | 44 | D. | 48 |
2.某公司对新研发的一种产品进行合理定价,且销量与单价具有相关关系,将该产品按事先拟定的价格进行试销,得到如下数据:
(1)现有三条y对x的回归直线方程:$\stackrel{∧}{y}$=-10x+170; $\stackrel{∧}{y}$=-20x+250; $\stackrel{∧}{y}$=-15x+210;根据所学的统计学知识,选择一条合理的回归直线,并说明理由.
(2)预计在今后的销售中,销量与单价服从(1)中选出的回归直线方程,且该产品的成本是每件5元,为使公司获得最大利润,该产品的单价应定多少元?(利润=销售收入-成本)
| 单价x(单位:元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y(单位:万件) | 90 | 84 | 83 | 80 | 75 | 68 |
(2)预计在今后的销售中,销量与单价服从(1)中选出的回归直线方程,且该产品的成本是每件5元,为使公司获得最大利润,该产品的单价应定多少元?(利润=销售收入-成本)