题目内容
在平面直角坐标系xOy中，设直线x+2y-2=0与圆x2+y2+6x-4y+11=0相交于A，B两点，则线段AB的长为 ．
考点：直线与圆的位置关系
专题：直线与圆
分析：由直线与圆相交的性质可知，（
）2=r2-d2，要求AB，只要求解圆心到直线x+2y-2=0的距离．
| AB |
| 2 |
解答：
解：由题意圆x2+y2+6x-4y+11=0可得，圆心（-3，2），半径r=
，圆心到直线x+2y-2=0的距离d=
=
，
则由圆的性质可得，（
）2=r2-d2=2-
=
，
即AB=
．
故答案为：
| 2 |
| |-3+4-2| | ||
|
| 1 | ||
|
则由圆的性质可得，（
| AB |
| 2 |
| 1 |
| 5 |
| 9 |
| 5 |
即AB=
6
| ||
| 5 |
故答案为：
6
| ||
| 5 |
点评：本题主要考查了直线与圆相交性质的应用，点到直线的距离公式的应用，属于基础试题，
练习册系列答案
相关题目
如图，一个类似杨辉三角的数阵，则
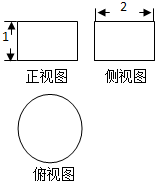如图所示，一个空间几何体的正视图和侧视图都是相邻两边的长分别为1和2的矩形，俯视图是一个圆，那么这个几何体的体积为（ ）| A、4π | ||
| B、π | ||
C、
| ||
D、
|