题目内容
已知数列{an}是首项为3，公差为1的等差数列，数列{bn}是首项为
，公比也为
的等比数列，其中n∈N*，那么数列{anbn}的前n项和Sn= ．
| 1 |
| 2 |
| 1 |
| 2 |
考点：等差数列与等比数列的综合
专题：计算题,等差数列与等比数列
分析：先确定数列{an}、{bn}的通项，可得数列{anbn}的通项，利用错位相减法，即可求出数列{anbn}的前n项和．
解答：
解：an=3+（n-1）=n+2，bn=
，
∴anbn=（n+2）•
，
∴Sn=3•
+4•
+…+（n+2）•
，
∴
Sn=3•
+4•
+…+（n+1）•
+（n+2）•
，
两式相减，化简可得Sn=4-
．
故答案为：4-
．
| 1 |
| 2n |
∴anbn=（n+2）•
| 1 |
| 2n |
∴Sn=3•
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n |
∴
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
| 1 |
| 2n+1 |
两式相减，化简可得Sn=4-
| n+4 |
| 2n |
故答案为：4-
| n+4 |
| 2n |
点评：本题考查数列的通项与求和，考查错位相减法，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
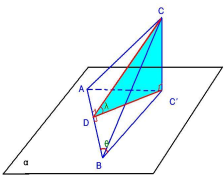如图，已知△ABC在平面α内的射影为△ABC′，若∠ABC′=θ，BC′=a，且平面ABC与平面α所成的角为λ，求点C到平面α的距离．