题目内容
证明:在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
考点:二项式系数的性质
专题:二项式定理
分析:在二项定理中,令a=1、b=-1,化简可得
+
+…=
+
+…,命题得证.
| C | 0 n |
| C | 2 n |
| C | 1 n |
| C | 3 n |
解答:
证明:在展开式中(a+b)n=
an+
an-1b+…+
an-rbr+…+
bn(n∈N+)中,
令a=1,b=-1,则(1-1)n=
-
+
-
+…+(-1)n
,
即0=(
+
+…)-(
+
+…),即
+
+…=
+
+…,
即在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
| C | 0 n |
| C | 1 n |
| C | r n |
| C | n n |
令a=1,b=-1,则(1-1)n=
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | n n |
即0=(
| C | 0 n |
| C | 2 n |
| C | 1 n |
| C | 3 n |
| C | 0 n |
| C | 2 n |
| C | 1 n |
| C | 3 n |
即在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
点评:本题主要考查二项式定理的应用,注意根据题意,分析所给代数式的特点,通过给二项式的x赋值,求展开式的系数和,可以简便的求出答案,属于基础题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
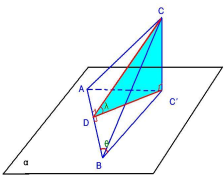 如图,已知△ABC在平面α内的射影为△ABC′,若∠ABC′=θ,BC′=a,且平面ABC与平面α所成的角为λ,求点C到平面α的距离.
如图,已知△ABC在平面α内的射影为△ABC′,若∠ABC′=θ,BC′=a,且平面ABC与平面α所成的角为λ,求点C到平面α的距离.