题目内容

已知（a2+a+
3
2
）x＞（a2+a+
3
2
）1-x，则实数x的取值范围
 
．
考点：根式与分数指数幂的互化及其化简运算
专题：函数的性质及应用
分析：利用指数函数的单调性即可得出．
解答： 解：∵a2+a+
3
2
=(a+
1
2
)2+
5
4
＞1，（a2+a+
3
2
）x＞（a2+a+
3
2
）1-x，
∴x＞1-x，解得x＞
1
2
．
∴实数x的取值范围是(
1
2
，+∞)．
故答案为：(
1
2
，+∞)．
点评：本题考查了指数函数的单调性，属于基础题．
练习册系列答案
相关题目
若对任意的实数m，n，都有f（m）+f（n）=f（m+n），且f（1007）=2，则f（1）+f（3）+f（5）+…+f（2013）=
 
．
若-
π
2
＜α＜0，则点Q（cosα，sinα）所在的象限是（　　）
A、一B、二C、三D、四
1°的圆心角所对弧长为1米，则此圆的半径为
 
．
点（-1，2）到直线y=x的距离是（　　）
A、
2
2
B、
3
2
2
C、
5
2
D、
1
2
已知7a=11b=A，且
1
a
+
1
b
=3，则A=
 
．
在△ABC中，
AB
=（2，3），
AC
=（1，k），且∠ABC=90°，求实数k的值．
设{an}是等差数列，前n项和为Sn，对任意m，k∈N*，都有
Sm
SK
=
m2
k2
，则
a4
a3
=
 
．
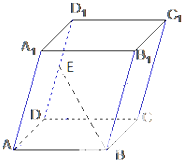如图，在平行六面体ABCD-A1B1C1D1中，AB=5，AD=3，AA1=4，∠DAB=90°∠BAA1=∠DAA1=60°E是DD的中点，设
AB
=
a
，
AD
=
b
，
AA1
=
c
．
（Ⅰ）用
a
，
b
，
c
表示
BE
；
（Ⅱ）求BE的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网