题目内容
已知向量 ,函数
,函数 ,且
,且 的图像过点
的图像过点 和点
和点 .
.
(1)求 的值;
的值;
(2)将 的图像向左平移
的图像向左平移 个单位后得到函数
个单位后得到函数 的图像,若
的图像,若 图像上各最高点到点
图像上各最高点到点 的距离的最小值为1,求
的距离的最小值为1,求 的解析式.
的解析式.
(1)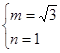 ;(2)
;(2)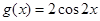 .
.
解析试题分析:
解题思路:(1)利用平面向量的数量积得出 ,再用待定系数法求出
,再用待定系数法求出 的值;(2)先根据图像变换得出变换后的解析式,再利用最高点到点
的值;(2)先根据图像变换得出变换后的解析式,再利用最高点到点 的距离的最小值为1求
的距离的最小值为1求 .
.
规律总结:涉及平面向量与三角函数的综合问题,往往以平面向量的平行、垂直、数量积为载体,使其转化成三角函数问题,再利用三角恒等变形与三角函数的图像与性质进行求解.
注意点: 的图像向左平移
的图像向左平移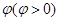 ,得到
,得到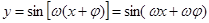 的图像.
的图像.
试题解析:(1)已知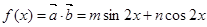 ,
,
因为 过点
过点
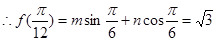
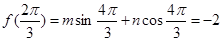
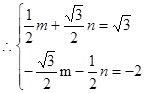
解得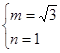
(2)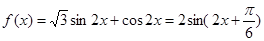
 左移
左移 后得到
后得到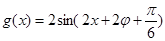
设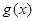 的对称轴为
的对称轴为 ,
,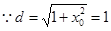 解得
解得
 ,解得
,解得
 .
.
考点:1.平面向量的数量积;2.三角函数的图像变换.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 .
. 的单调递增区间,最小正周期;
的单调递增区间,最小正周期;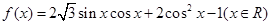 ,
,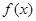 的最小正周期及在区间
的最小正周期及在区间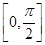 上的最大值和最小值;
上的最大值和最小值;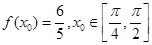 ,求
,求 的值.
的值. ,
, ,求sina的值.
,求sina的值. .
. ;
; 是第三象限角,且
是第三象限角,且 ,求
,求 的符号称二阶行列式,现规定
的符号称二阶行列式,现规定 , 函数
, 函数 =
= 在一个周期内的图象如图所示,
在一个周期内的图象如图所示, 为图象的最高点,
为图象的最高点,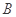 、
、 为图象与
为图象与 轴的交点,且
轴的交点,且 为正三角形。
为正三角形。 的值及函数
的值及函数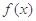 的单调递增区间;
的单调递增区间; ,在
,在 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.
 ,
, .
.  ;
; ,
,
 .
. 的最小正周期和单调递增区间;
的最小正周期和单调递增区间; ,求
,求 的值.
的值. 的顶点在坐标原点,始边写
的顶点在坐标原点,始边写 轴的正半轴重合,
轴的正半轴重合, ,角
,角 的终边与单位圆交点的横坐标是
的终边与单位圆交点的横坐标是 ,角
,角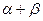 的终边与单位圆交点的纵坐标是
的终边与单位圆交点的纵坐标是 。
。