题目内容
将形如 的符号称二阶行列式,现规定
的符号称二阶行列式,现规定 , 函数
, 函数 =
= 在一个周期内的图象如图所示,
在一个周期内的图象如图所示, 为图象的最高点,
为图象的最高点,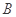 、
、 为图象与
为图象与 轴的交点,且
轴的交点,且 为正三角形。
为正三角形。
(1)求 的值及函数
的值及函数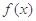 的单调递增区间;
的单调递增区间;
(2)若 ,在
,在 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.
(1)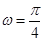 ,
,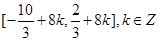 ;(2)
;(2)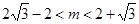 .
.
解析试题分析:解题思路:(1)利用定义的行列式化简 ,再结合图像,利用正三角形求
,再结合图像,利用正三角形求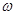 ;(2)将
;(2)将 在
在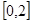 上恒成立,转化为
上恒成立,转化为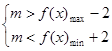 即可.规律总结:(1)对于新定义题目,要真正理解定义,想法与所学知识联系,是解决新定义题目的关键;三角函数的图像与性质要掌握好周期性、单调性;(2)不等式恒成立问题的一般思路是转化成求函数的最值问题.
即可.规律总结:(1)对于新定义题目,要真正理解定义,想法与所学知识联系,是解决新定义题目的关键;三角函数的图像与性质要掌握好周期性、单调性;(2)不等式恒成立问题的一般思路是转化成求函数的最值问题.
试题解析:(1)  =
=

=2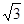 (
(
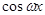 +
+
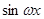 )=2
)=2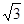
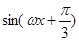
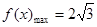 ∴BC=4,
∴BC=4,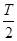 =4,T=8=
=4,T=8=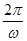 ,∴ω=
,∴ω= .
.
∴ f(x)=2
f(x)=2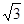 sin(
sin( x+
x+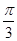 )
)
单调递增区间: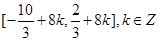 .
.
(2)依题意,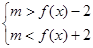 在x∈[0,2]时恒成立,
在x∈[0,2]时恒成立,
∴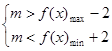 .
. 时,
时,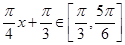 ,
,
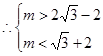 ,
, 即为所求.
即为所求.
考点:三角函数的图像与性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,面积
,面积 ,求这个扇形的半径
,求这个扇形的半径 和圆心角
和圆心角 的弧度数.
的弧度数. ,函数
,函数 ,且
,且 的图像过点
的图像过点 和点
和点 .
. 的值;
的值; 个单位后得到函数
个单位后得到函数 的图像,若
的图像,若 的距离的最小值为1,求
的距离的最小值为1,求
 的最小正周期;
的最小正周期; 时,若
时,若 ,求
,求 的值.
的值.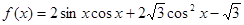 ,
,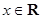 .
. 的最小正周期和单调递减区间;
的最小正周期和单调递减区间; 中的三个内角
中的三个内角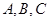 所对的边分别为
所对的边分别为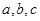 ,若锐角
,若锐角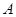 满足
满足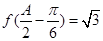 ,且
,且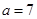 ,
,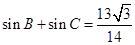 ,求
,求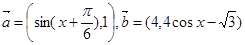
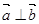 ,求
,求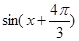 的值;
的值;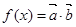 ,若
,若 ,求
,求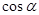 的值.
的值.  .
. 的最小正周期和最值;
的最小正周期和最值; , 求证:
, 求证: .
. ).
).
 ,1),F(
,1),F( ,
, ),求函数f(x)的解析式;
),求函数f(x)的解析式; )满足
)满足 ·
· =
= ,求函数f(x)的最大值.
,求函数f(x)的最大值. 为第三象限角,
为第三象限角, ,则
,则
