题目内容
已知函数 ,
,
 .
.
(1)求函数 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)若 ,求
,求 的值.
的值.
(1)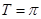 ,单调递增区间为
,单调递增区间为 ;(2)
;(2)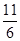 .
.
解析试题分析:(1)由题设可知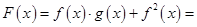
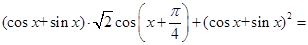
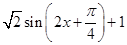
再利用正弦函数的性质求函数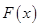 的最小正周期和单调区间;
的最小正周期和单调区间;
(2)由 ,再将
,再将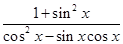 化成
化成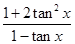 进而求值.
进而求值.
解:(1)易得 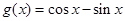
∴
=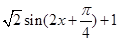 (3分)
(3分)
所以,函数 的最小正周期
的最小正周期
又由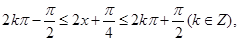
得: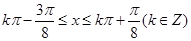
所以,函数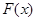 的单调递增区间为
的单调递增区间为
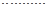 (6分)
(6分)
(2)由题意,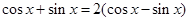
∴ (8分)
(8分)
所以,
 (12分)
(12分)
考点:1、两角和与差的三角函数公式;2、正弦函数的性质;3、同角三角函数的基本关系式.

练习册系列答案
相关题目
 ,函数
,函数 ,且
,且 的图像过点
的图像过点 和点
和点 .
. 的值;
的值; 个单位后得到函数
个单位后得到函数 的图像,若
的图像,若 的距离的最小值为1,求
的距离的最小值为1,求 .
. 的最小正周期和最值;
的最小正周期和最值; , 求证:
, 求证: .
.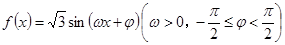 的图像关于直线
的图像关于直线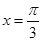 对称,且图像上相邻两个最高点的距离为
对称,且图像上相邻两个最高点的距离为 .
.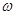 和
和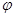 的值;
的值;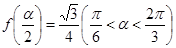 ,求
,求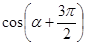 的值.
的值.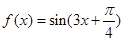 .
. 的单调递增区间;
的单调递增区间;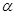 是第二象限角,
是第二象限角, ,求
,求 的值.
的值. 图象的一部分如图所示.
图象的一部分如图所示.
 的解析式;
的解析式; 时,求函数
时,求函数 的最大值与最小值及相应的
的最大值与最小值及相应的 的值.
的值. ).
).
 ,1),F(
,1),F( ,
, ),求函数f(x)的解析式;
),求函数f(x)的解析式; )满足
)满足 ·
· =
= ,求函数f(x)的最大值.
,求函数f(x)的最大值. 在
在 内只取到一个最大值和一个最小值,且当
内只取到一个最大值和一个最小值,且当 时,
时, ;当
;当 时,
时, .(1)求此函数的解析式;(2)求此函数的单调递增区间.
.(1)求此函数的解析式;(2)求此函数的单调递增区间.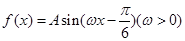 相邻两个对称轴之间的距离是
相邻两个对称轴之间的距离是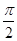 ,且满足,
,且满足,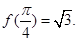
 的单调递减区间;
的单调递减区间; ,求△ABC的面积。
,求△ABC的面积。