题目内容
19.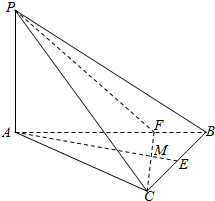 在三棱锥P-ABC中,PA⊥平面ABC,△ABC是直角三角形,AC⊥CB,PA=2,CA=2$\sqrt{3}$,CB=2,E为BC的中点,CF⊥AB于点F,CF交AE于点M.
在三棱锥P-ABC中,PA⊥平面ABC,△ABC是直角三角形,AC⊥CB,PA=2,CA=2$\sqrt{3}$,CB=2,E为BC的中点,CF⊥AB于点F,CF交AE于点M.(1)求二面角P-CF-B的余弦值;
(2)求点M到平面PBC的距离.
分析 (1)∠PFB是二面角P-CF-B的平面角,求出PF,BF,PB,利用余弦定理求二面角P-CF-B的余弦值;
(2)利用等体积求点M到平面PBC的距离.
解答 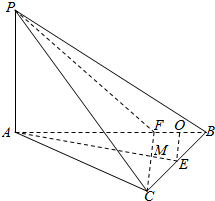 解:(1)∵CF⊥AB于点F,PA⊥平面ABC,
解:(1)∵CF⊥AB于点F,PA⊥平面ABC,
∴∠PFB是二面角P-CF-B的平面角.
∵AC⊥CB,PA=2,CA=2$\sqrt{3}$,CB=2,
∴AB=4
由射影定理可得12=AF•4,∴AF=3,
∴BF=1,
又PF=$\sqrt{4+9}$=$\sqrt{13}$,PB=$\sqrt{4+16}$=$\sqrt{20}$,
∴二面角P-CF-B的余弦值=$\frac{13+1-20}{2×\sqrt{13}×1}$=-$\frac{3\sqrt{13}}{13}$;
(2)取FB中点O,连接EO,由(1)可知,CF=$\sqrt{3}$,则EO=$\frac{\sqrt{3}}{2}$,MF=$\frac{3\sqrt{3}}{7}$,∴S△MBC=$\frac{1}{2}×\frac{4\sqrt{3}}{7}×1$=$\frac{2\sqrt{3}}{7}$
∵PA⊥平面ABC,AC⊥CB,
∴PC⊥CB,
∵PC=4,BC=2,∴S△PBC=$\frac{1}{2}×4×2$=4,
设点M到平面PBC的距离为h,则$\frac{1}{3}×4×h$=$\frac{1}{3}×\frac{2\sqrt{3}}{7}×2$,
∴h=$\frac{\sqrt{3}}{7}$.
点评 本题考查二面角P-CF-B的余弦值,点M到平面PBC的距离的求解,考查余弦定理,等体积的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
12.已知函数f(x)=$\frac{{e}^{x}}{{x}^{2}}$-k($\frac{2}{x}$+lnx),若x=2是函数f(x)的唯一一个极值点,则实数k的取值范围为( )
| A. | (-∞,e] | B. | [0,e] | C. | (-∞,e) | D. | [0,e) |
7.阅读如图的程序框图,运行相应的程序,输出n的值为( )


| A. | 5 | B. | 7 | C. | 9 | D. | 11 |
9.已知sin($\frac{π}{4}$+x)=$\frac{1}{4}$,则cos(x+$\frac{7π}{4}$)等于( )
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | $\frac{\sqrt{15}}{4}$ | D. | -$\frac{\sqrt{15}}{4}$ |



