题目内容
10.已知函数f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$,若不等式f(-2m2+2m-1)+f(8m+ek)>0(e是自然对数的底数),对任意的m∈[-2,4]恒成立,则整数k的最小值是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 根据条件判断函数的奇偶性和单调性,利用函数奇偶性和单调性的关系将不等式进行转化,利用参数分离法,转化求函数的最值即可.
解答 解:∵f(-x)=$\frac{{2}^{-x}-1}{{2}^{-x}+1}$=$\frac{1-{2}^{x}}{1+{2}^{x}}$=-$\frac{{2}^{x}-1}{{2}^{x}+1}$=-f(x),
∴函数f(x)是奇函数,
函数f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$.定义域为R,函数f(x)在R上是增函数.
证明:设x1,x2是R内任意两个值,且x1<x2.
则$f({x_1})-f({x_2})=\frac{{{2^{x_1}}-1}}{{{2^{x_1}}+1}}-\frac{{{2^{x_2}}-1}}{{{2^{x_2}}+1}}$=$\frac{2({2}^{{x}_{1}}-{2}^{{x}_{2}})}{({2}^{{x}_{1}}+1)({2}^{{x}_{2}}+1)}$①.
又因为x1<x2,所以${2}^{{x}_{1}}<{2}^{{x}_{2}}$,又${2}^{{x}_{1}}+1>0,{2}^{{x}_{2}}+1>0$.
所以①<0,即f(x1)-f(x2)<0,即f(x1)<f(x2).
故f(x)是R上的增函数.
则不等式若不等式f(-2m2+2m-1)+f(8m+ek)>0等价为若不等式f(8m+ek)>-f(-2m2+2m-1)=f(2m2-2m+1),
即8m+ek>2m2-2m+1,
即ek>2m2-10m+1,
设g(m)=2m2-10m+1,则函数的对称轴为m=$-\frac{-10}{2×2}$=$\frac{5}{2}$,
则当m∈[-2,4]时,当m=-2时,函数g(m)取得最大值g(-2)=29,
即ek>g(m)max=29,
则k>ln29.
∵k是整数,
∴k的最小值是4,
故选:C.
点评 本题考查不等式恒成立问题,根据条件判断函数的奇偶性和单调性是解决本题的关键.,利用转化法和参数分离法是解决不等式恒成立问题的思路.

| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
| A. | ?x∈R,x2+5x≥6 | B. | ?x∈R,x2+5x=6 | C. | ?x0∈R,x02+5x0≥6 | D. | ?x∈R,x02+5x0<6 |
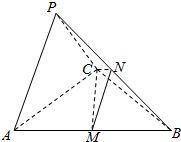 如图,在三棱锥P-ABC中,底面ABC是边长为4的正三角形,PA=PC=2$\sqrt{3}$,侧面PAC⊥底面ABC,M,N分别为AB、PB的中点.
如图,在三棱锥P-ABC中,底面ABC是边长为4的正三角形,PA=PC=2$\sqrt{3}$,侧面PAC⊥底面ABC,M,N分别为AB、PB的中点.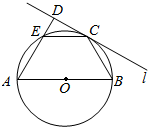 如图,AB是圆O的直径,C为圆周上一点,过C作圆O的切线l,过A作直线l的垂线AD,D为垂足,AD与圆O交于点E.
如图,AB是圆O的直径,C为圆周上一点,过C作圆O的切线l,过A作直线l的垂线AD,D为垂足,AD与圆O交于点E.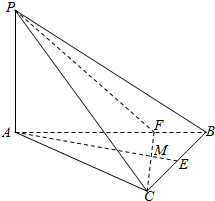 在三棱锥P-ABC中,PA⊥平面ABC,△ABC是直角三角形,AC⊥CB,PA=2,CA=2$\sqrt{3}$,CB=2,E为BC的中点,CF⊥AB于点F,CF交AE于点M.
在三棱锥P-ABC中,PA⊥平面ABC,△ABC是直角三角形,AC⊥CB,PA=2,CA=2$\sqrt{3}$,CB=2,E为BC的中点,CF⊥AB于点F,CF交AE于点M.