题目内容

14．如图，每个函数图象都有零点，但不能用二分法求图中函数零点的是（　　）
A．B．C．D．

分析 根据二分法求零点的原理可判断．

解答 解：由二分法的定义可知若存在区间[a，b]，使得f（x）在[a，b]上连续，且f（a）•f（b）＜0，则f（x）在（a，b）上有零点．
显然A，B，D符合条件．对于C，由于f（x）≥0，故不存在区间[a，b]使得f（a）•f（b）＜0．
故选C．

点评 本题考查了二分法的定义，零点的存在性定理，属于基础题．

练习册系列答案
相关题目
7．已知O是坐标原点，点A的坐标为（2，1），若点B（x，y）为平面区域$\left\{\begin{array}{l}x+y≤4\\ x≥1\\ y≥x\end{array}\right.$上的一个动点，则z=$\overrightarrow{OA}$•$\overrightarrow{OB}$的最大值是6．
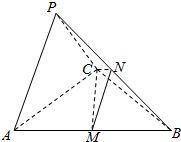5．如图，在三棱锥P-ABC中，底面ABC是边长为4的正三角形，PA=PC=2$\sqrt{3}$，侧面PAC⊥底面ABC，M，N分别为AB、PB的中点．
（Ⅰ）求证：AC⊥PB；
（Ⅱ）求二面角N-CM-B的大小的余弦值．
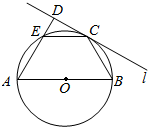2．如图，AB是圆O的直径，C为圆周上一点，过C作圆O的切线l，过A作直线l的垂线AD，D为垂足，AD与圆O交于点E．
（1）求证：AB•DE=BC•CE；
（2）若AB=8，BC=4，求线段AE的长．
9．设等差数列{an}的前n项和为Sn，且S4=4S2，a2+a4=10．
（1）求数列{an}通项公式；
（2）若数列{bn}满足$\frac{{b}_{1}}{{a}_{1}}$+$\frac{{b}_{2}}{{a}_{2}}$+…+$\frac{{b}_{n}}{{a}_{n}}$=1-$\frac{1}{{2}^{n}}$，n∈N*，求数列{bn}的前n项和Tn．
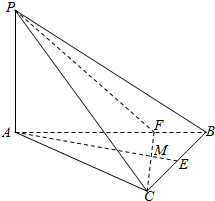19．在三棱锥P-ABC中，PA⊥平面ABC，△ABC是直角三角形，AC⊥CB，PA=2，CA=2$\sqrt{3}$，CB=2，E为BC的中点，CF⊥AB于点F，CF交AE于点M．
（1）求二面角P-CF-B的余弦值；
（2）求点M到平面PBC的距离．
6．设f′（x）是f（x）=$\frac{1-x}{1+x}$的导数，则$\frac{f′（3）}{f（3）}$=（　　）
A．$\frac{1}{4}$B．0C．-$\frac{3}{4}$D．1
3．直线l过点M（-1，2），且与以P（-4，-1），Q（3，0）为端点的线段相交，则直线l的斜率的取值范围（　　）
A．[-$\frac{1}{2}$，1]B．[-2，1]C．（-∞，-2]∪[1，+∞）D．（-∞，-$\frac{1}{2}$]∪[1，+∞）
4．函数y=$\frac{1}{x}$在x=$\frac{1}{2}$处的切线与两坐标轴所围成图形的面积是（　　）
A．2B．3C．$\frac{3}{2}$D．$\frac{5}{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网