题目内容
16．f（x）在R上为奇函数，且当x＞0时f（x）=x-1，则当x＜0时f（x）=x+1．分析 根据函数奇偶性的性质进行转化求解即可．
解答 解：∵f（x）在R上为奇函数，且当x＞0时f（x）=x-1，
∴当x＜0，则-x＞0，
则f（-x）=-x-1=-f（x），
则f（x）=x+1，
故答案为：x+1
点评 本题主要考查函数解析式的求解，根据函数奇偶性的性质进行转化是解决本题的关键．
练习册系列答案
期末100分闯关海淀考王系列答案
小学能力测试卷系列答案
相关题目
20．设a，b是两条直线α，β是两个平面，则“a?α，b⊥β，α∥β”是“a⊥b”的（ ）
| A． | 必要不充分条件 | B． | 充要条件 | ||
| C． | 充分不必要条件 | D． | 既不充分也不必要条件 |
8．下列函数中，值域为（0，+∞）的是（ ）
| A． | y=$\sqrt{x}$ | B． | $y=\frac{1}{{\sqrt{x}}}$ | C． | $y=\frac{1}{x}$ | D． | y=x2+x+1 |
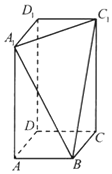长方体ABCD-A1B1C1D1中，AB=BC=2，过A1，C1，B三点的平面截去长方体的一个角后，得到如图所示的几何体ABCD-A1C1D1，这个几何体的体积为$\frac{40}{3}$