题目内容
3.某几何体的三视图如图所示,则该几何体的表面积为( )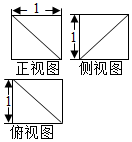
| A. | $\frac{5}{6}$ | B. | 6 | C. | 3+$\sqrt{3}$ | D. | $\frac{9+\sqrt{3}}{2}$ |
分析 几何体为正方体切去一个三棱锥后剩余的部分.
解答  解:由三视图可知几何体为正方体ABCD-A'B'C'D'切去一个三棱锥B'-A'BC'得到的,
解:由三视图可知几何体为正方体ABCD-A'B'C'D'切去一个三棱锥B'-A'BC'得到的,
正方体的棱长为1,切去的三棱锥的底面A'BC'是边长为$\sqrt{2}$的等边三角形.
所以几何体的表面积S=12×3+$\frac{1}{2}×{1}^{2}×3$+$\frac{\sqrt{3}}{4}×(\sqrt{2})^{2}$=$\frac{9+\sqrt{3}}{2}$,
故选D.
点评 本题考查了不规则几何体的三视图和面积计算,以正方体为载体作出几何体的直观图是解题关键.

练习册系列答案
相关题目
14.$\frac{2}{1+i}-\frac{1+i}{2}$=( )
| A. | $\frac{1}{2}+\frac{1}{2}i$ | B. | $\frac{1}{2}-\frac{1}{2}i$ | C. | $\frac{1}{2}+\frac{3}{2}i$ | D. | $\frac{1}{2}-\frac{3}{2}i$ |
11.已知a,b∈(0,1),则函数f(x)=ax2-4bx+1在区间[1,+∞)上是增函数的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{5}$ |
8.若偶函数f(x)在(-∞,0]上单调递减,a=f(log23),b=f(-1),c=f(2${\;}^{\frac{3}{2}}$),则a,b,c满足( )
| A. | a<b<c | B. | b<a<c | C. | c<a<b | D. | c<b<a |
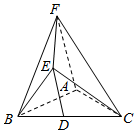 在如图所示的几何体EFABC中,已知△ABC是等腰三角形,AB=AC,AF⊥平面ABC,D为BC的中点,DE∥AF且BC=AF=2DE=2.
在如图所示的几何体EFABC中,已知△ABC是等腰三角形,AB=AC,AF⊥平面ABC,D为BC的中点,DE∥AF且BC=AF=2DE=2.