题目内容
18.在平面直角坐标系xOy中,已知三圆C1:x2+y2=4,C2:(x+$\sqrt{3}$)2+(y-1)2=4,C3:$\left\{\begin{array}{l}{x=\sqrt{3}+2cosθ}\\{y=1+2sinθ}\end{array}\right.$(θ为参数)有一公共点P(0,2).(Ⅰ)分别求C1与C2,C1与C3异于点P的公共点M、N的直角坐标;
(Ⅱ)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求经过三点O、M、N的圆C的极坐标方程.
分析 (1)求出圆C3的普通方程,解方程组得出交点坐标;
(2)求出过三点的圆的普通方程,转化为极坐标方程.
解答 解:(I)圆C3的直角坐标方程为(x-$\sqrt{3}$)2+(y-1)2=4.
联立方程组$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=4}\\{(x+\sqrt{3})^{2}+(y-1)^{2}=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=0}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\sqrt{3}}\\{y=-1}\end{array}\right.$.
联立方程组$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=4}\\{(x-\sqrt{3})^{2}+(y-1)^{2}=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=0}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=\sqrt{3}}\\{y=-1}\end{array}\right.$.
∴M(-$\sqrt{3}$,-1),N($\sqrt{3}$,-1).
(II)M,N的中垂线方程为x=0,故过点M,N,O三点的圆圆心在y轴上,设圆的半径为r,
则(r-1)2+$(\sqrt{3})^{2}$=r2,解得r=2.∴圆心坐标为(0,-2).
∴经过三点O、M、N的圆C的直角坐标方程为x2+(y+2)2=4.即x2+y2+4y=0.
∴经过三点O、M、N的圆C的极坐标方程为ρ2+4ρsinθ=0,即ρ=-4sinθ.
点评 本题考查了参数方程,极坐标方程与普通方程的转化,考查学生的空间想象和运算求解能力.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案| A. | $-\frac{1}{5}$ | B. | $-\frac{1}{5}i$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{5}i$ |
| A. | (-1,3) | B. | (-1,2) | C. | (0,2) | D. | [2.3) |
| A. | -3 | B. | -2 | C. | $\frac{2\sqrt{3}}{3}$ | D. | 3 |
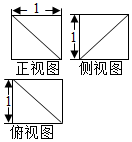
| A. | $\frac{5}{6}$ | B. | 6 | C. | 3+$\sqrt{3}$ | D. | $\frac{9+\sqrt{3}}{2}$ |
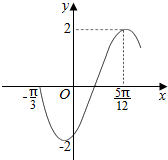
| A. | 2,-$\frac{π}{3}$ | B. | 2,-$\frac{π}{6}$ | C. | 4,-$\frac{π}{6}$ | D. | 4,$\frac{π}{3}$ |
| A. | f(x)≥2-4ln2 | B. | f(x)≤2-4ln2 | C. | f(x)≥4-8ln2 | D. | f(x)≤4-8ln2 |