题目内容
15.已知f(x)=|x-1|+|2x+3|.(1)若f(x)≥m对一切x∈R都成立,求实数m的取值范围;
(2)解不等式f(x)≤4.
分析 (1)通过讨论x的范围,求出f(x)的最小值,从而求出m的范围即可;(2)求出各个区间上的不等式的解集,取并集即可.
解答 解:(1)f(x)=|x-1|+|2x+3|,
x≥1时,f(x)=x-1+2x+3=3x+2,f(x)≥5,
-$\frac{3}{2}$<x<1时,f(x)=-x+1+2x+3=x+4,$\frac{5}{2}$<f(x)<5,
x≤-$\frac{3}{2}$时,f(x)=-x+1-2x-3=-3x-2≥$\frac{5}{2}$,
若f(x)≥m对一切x∈R都成立,
只需m≤$\frac{5}{2}$即可;
(2)x≥1时,f(x)=x-1+2x+3=3x+2≤4,解得:x≤$\frac{2}{3}$,无解,
-$\frac{3}{2}$<x<1时,f(x)=-x+1+2x+3=x+4≤4,解得:x≤0,
x≤-$\frac{3}{2}$时,f(x)=-x+1-2x-3=-3x-2≤4,解得:x≥-2,
故不等式的解集是:[-2,0].
点评 本题考查了绝对值不等式问题,考查分类讨论思想,是一道中档题.

练习册系列答案
相关题目
5.阅读如图所示的程序框图,运行相应的程序,若输入n的值为4,则输出S的值为( )
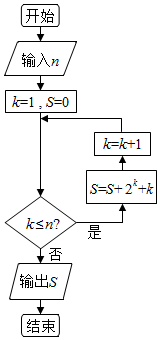

| A. | 20 | B. | 40 | C. | 77 | D. | 546 |
6.已知集合A={x|-1<x<2},B={x|x2-3x<0},则∁RA∩B=( )
| A. | (-1,3) | B. | (-1,2) | C. | (0,2) | D. | [2.3) |
3.某几何体的三视图如图所示,则该几何体的表面积为( )
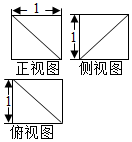

| A. | $\frac{5}{6}$ | B. | 6 | C. | 3+$\sqrt{3}$ | D. | $\frac{9+\sqrt{3}}{2}$ |
7.函数f(x)=2sin(ωx+φ)的部分图象如图所示,则ω,φ的值分别是( )
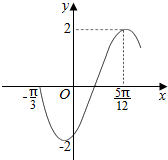

| A. | 2,-$\frac{π}{3}$ | B. | 2,-$\frac{π}{6}$ | C. | 4,-$\frac{π}{6}$ | D. | 4,$\frac{π}{3}$ |
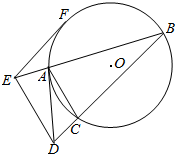 如图所示,△ABC内接于⊙O,直线AD与⊙O相切于点A,交BC的延长线于点D,过点D作DE∥CA交BA的延长线于点E.
如图所示,△ABC内接于⊙O,直线AD与⊙O相切于点A,交BC的延长线于点D,过点D作DE∥CA交BA的延长线于点E.