题目内容
11.已知a,b∈(0,1),则函数f(x)=ax2-4bx+1在区间[1,+∞)上是增函数的概率为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{5}$ |
分析 根据题意,a、b是从区间(0,2)上任取的数,故有无穷多种取法,在平面坐标系内作出a、b对应的区域为一正方形.函数f(x)=ax2-4bx+1在[1,+∞)上递增,由二次函数的单调性可得到a和b的关系,作出在平面坐标系内对应的区域,由几何概型面积之比求概率即可
解答 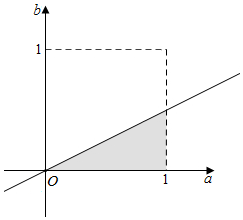 【解答】解:函数f(x)在[1,+∞)上递增,由二次函数的单调性可知
【解答】解:函数f(x)在[1,+∞)上递增,由二次函数的单调性可知
-$\frac{-4b}{2a}$=$\frac{2b}{a}$≤1,即a≥2b.
由题意得$\left\{\begin{array}{l}{0<a<1}\\{0<b<1}\\{a>2b}\end{array}\right.$,画出图示得阴影部分面积.
∴概率为$\frac{\frac{1}{2}×1×\frac{1}{2}}{1×1}$=$\frac{1}{4}$,
故选:A.
点评 本题考查几何概型的求法、二元一次不等式组表示的平面区域,考查数形集合思想解题.

练习册系列答案
相关题目
2.已知函数$f(x)=\frac{1}{2}{x^2}+mlnx-2x$在定义域内是增函数,则实数m的取值范围是( )
| A. | m≤1 | B. | m≥1 | C. | m<1 | D. | m>1 |
6.已知集合A={x|-1<x<2},B={x|x2-3x<0},则∁RA∩B=( )
| A. | (-1,3) | B. | (-1,2) | C. | (0,2) | D. | [2.3) |
3.某几何体的三视图如图所示,则该几何体的表面积为( )
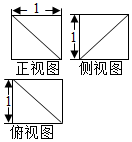

| A. | $\frac{5}{6}$ | B. | 6 | C. | 3+$\sqrt{3}$ | D. | $\frac{9+\sqrt{3}}{2}$ |
1.已知点P在直线x+3y-2=0上,点Q在直线x+3y+6=0上,线段PQ的中点为M(x0,y0),且y0<x0+2,则$\frac{y_0}{x_0}$的取值范围是( )
| A. | [-$\frac{1}{3}$,0) | B. | (-$\frac{1}{3}$,0) | C. | (-$\frac{1}{3}$,+∞) | D. | (-∞,-$\frac{1}{3}$)∪(0,+∞) |