题目内容
9.一种新款手机的价格原来是a元,在今后m个月内,价格平均每月减少p%,则这款手机的价格y元随月数x变化的函数解析式:y=a(1-p%)x(0≤x≤m).分析 分别取x=1,2,3,得出相应的价格表达式,归纳出,经过x个月后,价格为:a(1-p%)x,x≤m.
解答 解:根据题意,因为原价为a元,价格每月减少p%,因此,
经过以一个月后(x=1),价格为:a(1-p%),
再过一个月后(x=2),价格为:a(1-p%)(1-p%),
再过一个月后(x=3),价格为:a(1-p%)(1-p%)(1-p%),
…
经过x个月后,价格为:a(1-p%)x,x≤m,
所以,价格y元随月数x变化的函数解析式为:y=a(1-p%)x(0≤x≤m).
故答案为:y=a(1-p%)x(0≤x≤m).
点评 本题主要考查了函数解析式的求解及常用方法,通过自变量x=1,2,3,观察出表达式的特征,归纳出函数的解析式,属于基础题.

练习册系列答案
相关题目
19.春节前,某市一过江大桥上挂了两串彩灯,这两串彩灯的第一次闪亮相互独立,且都在通电后的6秒内任一时刻等可能发生,然后每串彩灯以6秒内间隔闪亮,那么这两串彩灯同时通电后,它们第一次闪亮的时刻相差不超过3秒的概率是( )
| A. | $\frac{7}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
1.如图可能是下列哪个函数的图象( )
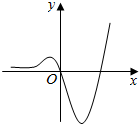

| A. | y=2x-x2-1 | B. | y=$\frac{x}{lnx}$ | C. | y=$\frac{{2}^{x}sinx}{{4}^{x}+1}$ | D. | y=(x2-2x)ex |
18.M是椭圆$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1上一点,F1,F2是椭圆的左、右焦点,I是△MF1F2的内心,延长MI交F1F2于N,则$\frac{|MI|}{|IN|}$等于( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 1 |