题目内容
 如图,在智利地震灾区的搜救现场,一条搜救狗沿正北方向行进xm发现生命迹象,然后向右转105°,行进10m发现另一生命迹象,这时它向右转135°后续继前行回到出发点,那么x=
如图,在智利地震灾区的搜救现场,一条搜救狗沿正北方向行进xm发现生命迹象,然后向右转105°,行进10m发现另一生命迹象,这时它向右转135°后续继前行回到出发点,那么x=考点:解三角形的实际应用
专题:应用题,解三角形
分析:先画出简图,得到各角的值,再由正弦定理可确定答案.
解答:
解:由题意可得简图如下
可知∠ABC=75°,∠ACB=45°,∠A=60°,
根据正弦定理可得:
=
,
∴x=
.
故答案为:
.
可知∠ABC=75°,∠ACB=45°,∠A=60°,
根据正弦定理可得:
| x |
| sin∠ACB |
| 10 |
| sinA |
∴x=
10
| ||
| 3 |
故答案为:
10
| ||
| 3 |
点评:本题主要考查正弦定理的应用,关键在于能够画出简图.属基础题.

练习册系列答案
相关题目
确定结论“X与Y有关系”的可信度为99%时,则随即变量k2的观测值k必须( )
| A、大于10.828 |
| B、大于7.879 |
| C、大于6.635 |
| D、大于2.706 |
已知圆的方程为x2+y2-6x-8y=0,设该圆内过点 (-3,5)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为( )
A、10
| ||
B、20
| ||
C、30
| ||
D、40
|
将周期为π的函数y=sin2ωx+2sinωxcosωx-cos2ωx(ω>0)的图象按
=(-
,1)平移后,所得函数图象的解析式为( )
| a |
| π |
| 8 |
A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=1-
|
己知关于x的方程(m+3)x2-4mx+2m-1=0 的两根异号,且负根的绝对值比正根大,那么实数m的取值范围是( )
| A、-3<m<0 |
| B、0<m<3 |
| C、m<-3或m>0 |
| D、m<0 或 m>3 |
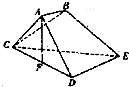 已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2a,AB=a,F为CD的中点.
已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2a,AB=a,F为CD的中点.