题目内容
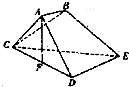 已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2a,AB=a,F为CD的中点.
已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2a,AB=a,F为CD的中点.(1)求证:AF⊥平面CDE;
(2)求异面直线AC,BE所成角的余弦值;
(3)求多面体ABCDE的体积.
考点:棱柱、棱锥、棱台的体积,异面直线及其所成的角,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)由已知得DE⊥AF.AF⊥CD,由此能证明AF⊥平面CDE.
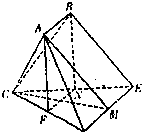
(2)由已知得DE∥AB,取DE中点M,连结AM、CM,则四边形AMEB为平行四边形,AM∥BE,则∠CAM为AC与BE所成的角,由此能求出异面直线AC、BE所成的角的余弦值.
(3)取CE的中点N,连结BN、FN,四边形AFNB为平行四边形,由此能求出多面体ABCDE的体积.
(2)由已知得DE∥AB,取DE中点M,连结AM、CM,则四边形AMEB为平行四边形,AM∥BE,则∠CAM为AC与BE所成的角,由此能求出异面直线AC、BE所成的角的余弦值.
(3)取CE的中点N,连结BN、FN,四边形AFNB为平行四边形,由此能求出多面体ABCDE的体积.
解答:
(1)证明:∵DE⊥平面ACD,AF?平面ACD,∴DE⊥AF.
又∵AC=AD,F为CD中点,
∴AF⊥CD,∴AF⊥平面CDE.
(2)解:
⇒DE∥AB,
取DE中点M,连结AM、CM,则四边形AMEB为平行四边形.
AM∥BE,则∠CAM为AC与BE所成的角,
在△ACM中,AC=2a,
∴异面直线AC、BE所成的角的余弦值为
.
(3)解:取CE的中点N,连结BN、FN,则FN
DE,
又AB
DE,则四边形AFNB为平行四边形.
∴AF∥BN,又由(1)知,AF⊥面CDE,∴BN⊥面CDE.
又∵AC=AD,F为CD中点,
∴AF⊥CD,∴AF⊥平面CDE.
(2)解:
|
取DE中点M,连结AM、CM,则四边形AMEB为平行四边形.
AM∥BE,则∠CAM为AC与BE所成的角,
在△ACM中,AC=2a,

|
∴异面直线AC、BE所成的角的余弦值为
| ||
| 5 |
(3)解:取CE的中点N,连结BN、FN,则FN
| ∥ |
. |
| 1 |
| 2 |
又AB
| ∥ |
. |
| 1 |
| 2 |
∴AF∥BN,又由(1)知,AF⊥面CDE,∴BN⊥面CDE.
|
点评:本题考查AF⊥平面CDE的证明,考查异面直线AC,BE所成角的余弦值的求法,考查多面体ABCDE的体积的求法,解题时要注意空间思维能力的培养.

练习册系列答案
相关题目
设数列{an} 的前n项和为 Sn,令Tn=
,称 Tn为数列 a1,a2,…,an的“理想数“,已知数列a1,a2,…,a20的“理想数“为21,那么数列2,a1,a2,…,a20 的“理想数”为( )
| S1+S2+…+Sn |
| n |
| A、23 | B、24 | C、22 | D、20 |
已知不等式|x-m|<1成立的一个充分非必要条件是
<x<
,则实数m的取值范围是( )
| 1 |
| 3 |
| 1 |
| 2 |
A、[-
| ||||
B、[-
| ||||
C、(-∞,-
| ||||
D、[
|

 如图,在智利地震灾区的搜救现场,一条搜救狗沿正北方向行进xm发现生命迹象,然后向右转105°,行进10m发现另一生命迹象,这时它向右转135°后续继前行回到出发点,那么x=
如图,在智利地震灾区的搜救现场,一条搜救狗沿正北方向行进xm发现生命迹象,然后向右转105°,行进10m发现另一生命迹象,这时它向右转135°后续继前行回到出发点,那么x=