题目内容
13.Sn表示数列{an}(n≥1)的前n项和,已知a1=1,且?n≥1,Sn+1=4an+2,则a2013等于( )| A. | 3019•22012 | B. | 3019•22013 | C. | 3018•22012 | D. | 以上答案均不对 |
分析 Sn+1=4an+2,a1=1,可得a2=5,Sn=4an-1+2,可得:an+1-2an=2(an-2an-1),利用等比数列的通项公式可得:an-2an-1=3×2n-2,(n≥2).
变形为$\frac{{a}_{n}}{{2}^{n}}$-$\frac{{a}_{n-1}}{{2}^{n-1}}$=$\frac{3}{4}$,再利用等差数列的通项公式即可得出.
解答 解:∵Sn+1=4an+2,a1=1,
∴a2=5,Sn=4an-1+2,
可得:an+1=4an-4an-1,
变形为:an+1-2an=2(an-2an-1),
∴数列{an-2an-1}是等比数列,首项为3,公比为2.
∴an-2an-1=3×2n-2,(n≥2).
∴$\frac{{a}_{n}}{{2}^{n}}$-$\frac{{a}_{n-1}}{{2}^{n-1}}$=$\frac{3}{4}$,
∴数列$\{\frac{{a}_{n}}{{2}^{n}}\}$是等差数列,首项为$\frac{1}{2}$,公差为$\frac{3}{4}$.
∴$\frac{{a}_{n}}{{2}^{n}}$=$\frac{1}{2}+\frac{3}{4}(n-1)$=$\frac{3n-1}{4}$,
∴an=(3n-1)×2n-2.
∴a2013=3019×22012.
故选:A.
点评 本题考查了等比数列与等比数列的通项公式、递推关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.已知圆C:(x-1)2+(y-2)2=2截y轴所得线段与截直线y=2x+b所得线段的长度相等,则b=( )
| A. | $-\sqrt{6}$ | B. | ±$\sqrt{6}$ | C. | $-\sqrt{5}$ | D. | ±$\sqrt{5}$ |
5.若等比数列{an}的公比为q,n为偶数,则数列的第$\frac{n}{2}$项为( )
| A. | a1q${\;}^{\frac{n}{2}}$ | B. | a1q${\;}^{\frac{n-2}{2}}$ | C. | a1q${\;}^{\frac{n-1}{2}}$ | D. | a1q${\;}^{\frac{n}{2}+1}$ |
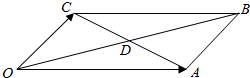 在下图平行四边形?OABC中,两对角线OB与AC相交于点D,若$\overrightarrow{OA}$=(3,1),$\overrightarrow{OC}$=(1,3),则向量$\overrightarrow{OD}$的坐标是(2,2).
在下图平行四边形?OABC中,两对角线OB与AC相交于点D,若$\overrightarrow{OA}$=(3,1),$\overrightarrow{OC}$=(1,3),则向量$\overrightarrow{OD}$的坐标是(2,2).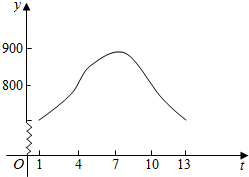 某地昆虫种群数量在七月份1~13日的变化如图所示,且满足y=Asin(ωx+φ)(ω>0,φ<0).
某地昆虫种群数量在七月份1~13日的变化如图所示,且满足y=Asin(ωx+φ)(ω>0,φ<0).