题目内容
(本小题满分12分)己知函数
(1)讨论函数f(x)的单调性;
(2)设 ,若对任意不相等的正数
,若对任意不相等的正数 ,恒有
,恒有 ,求a的取值范围.
,求a的取值范围.
(1)当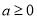 时,
时, 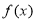 在
在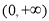 单调递增;当
单调递增;当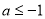 时,
时, 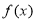 在
在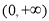 单调递减;
单调递减;
当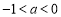 时,
时,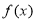 在
在 单调递增,在
单调递增,在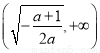 单调递减;(2)
单调递减;(2)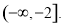
【解析】
试题分析:(1)先确定函数的定义域然后求导数fˊ(x),在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0,求出单调区间.
(2)根据第一问的单调性先对
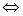
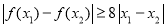 进行化简整理,转化成研究
进行化简整理,转化成研究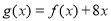 在(0,+∞)单调减函数,再利用参数分离法求出a的范围.
在(0,+∞)单调减函数,再利用参数分离法求出a的范围.
试题解析: (1)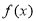 的定义域为
的定义域为 .
.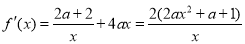
当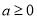 时,
时,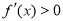 ,故
,故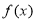 在
在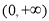 单调递增
单调递增
当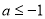 时,
时,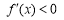 ,故
,故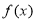 在
在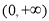 单调递减;
单调递减;
当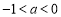 时,令
时,令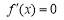 ,解得
,解得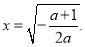
即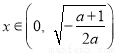 时,
时,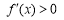 ;
; 时,
时,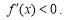 ;
;
故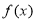 在
在 单调递增,在
单调递增,在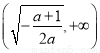 单调递减; 6分
单调递减; 6分
(2)不妨设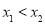 ,而
,而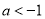 ,由(1)知
,由(1)知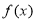 在
在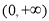 单调递减,从而对任意
单调递减,从而对任意 ,恒有
,恒有

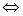
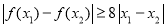
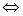
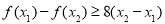
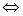
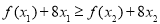 8分
8分
令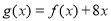 ,则
,则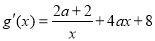
原不等式等价于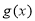 在
在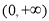 单调递减,即
单调递减,即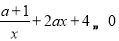 ,
,
从而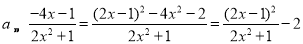 ,
,
故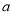 的取值范围为
的取值范围为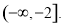 .12分
.12分
(如果考生将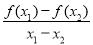 视为斜率,利用数形结合得到正确结果的,则总得分不超过8分)
视为斜率,利用数形结合得到正确结果的,则总得分不超过8分)
考点:利用导数研究函数的单调性.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
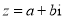
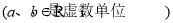 ,
,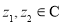 ,定义:
,定义: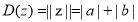 ,
,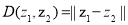 .给出下列命题:
.给出下列命题: 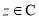 ,都有
,都有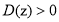 ;
;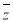 是复数
是复数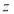 的共轭复数,则
的共轭复数,则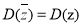 恒成立;
恒成立;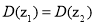
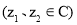 ,则
,则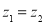 ;
;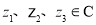 ,结论
,结论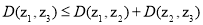 恒成立,则其中真命题是[答]( ).
恒成立,则其中真命题是[答]( ).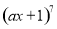 的展开式中,
的展开式中,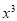 项的系数是
项的系数是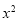 项系数和
项系数和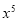 项系数的等比中项,则实数
项系数的等比中项,则实数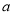 的值为
的值为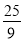 B.
B.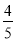 C.
C.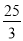 D.
D.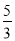
 是定义域为
是定义域为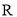 的偶函数. 当
的偶函数. 当 时,
时, 若关于
若关于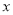 的方程
的方程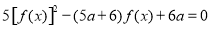 (
( ),有且仅有6个不同实数根,则实数
),有且仅有6个不同实数根,则实数 的取值范围是( )
的取值范围是( ) B.
B.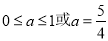
 D.
D. 或
或
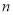 值等于7,则输出的
值等于7,则输出的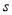 的值为( )
的值为( )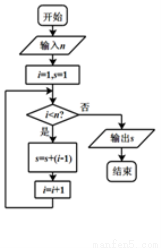
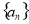 中,
中,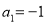 ,公差
,公差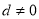 且
且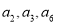 成等比数列,前
成等比数列,前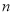 项的和为
项的和为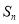 .
.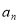 及
及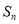 ;
;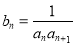 ,
,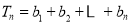 ,求
,求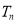 .
.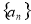 中,前10项的和等于前5项的和.若
中,前10项的和等于前5项的和.若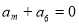 则
则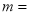 ( )
( )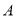 .10
.10 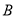 .9
.9 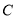 .8
.8 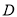 .2
.2
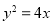 ,则其焦点到准线的距离为________.
,则其焦点到准线的距离为________.