题目内容
设集合A={x|-2＜x＜4}，B={x|x2-3ax+2a2＜0}，若B⊆A，求实数a的范围．
考点：集合的包含关系判断及应用
专题：集合
分析：将集合B化简，根据集合的包含关系分类判断即可．
解答：
解：∵A={x|-2＜x＜4}，B={x|x2-3ax+2a2＜0}={x|（x-a）（x-2a）＜0}，∴要使B⊆A，需对a进行讨论：
（1）当a＜0时，B=（2a，a），∴
?-1≤a≤2，得-1≤a＜0
（2）当a=0时，B=∅，满足题意
（3）当a＞0时，B=（a，2a），∴
?-2≤a≤2，得0≤a≤2
综上，a的取值范围是[-1，2]
故答案为：[-1，2]
（1）当a＜0时，B=（2a，a），∴
|
（2）当a=0时，B=∅，满足题意
（3）当a＞0时，B=（a，2a），∴
|
综上，a的取值范围是[-1，2]
故答案为：[-1，2]
点评：本题考查了集合的包含关系属于基础题．
练习册系列答案
同步练习强化拓展系列答案
相关题目
下列函数中，值域是（0，+∞）的函数是（ ）
A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=（
|
不等式|x-m|＜1的充分不必要条件是“
＜x＜
”，则实数m的取值范围是（ ）
| 1 |
| 3 |
| 1 |
| 2 |
A、[-
| ||||
B、(-∞，-
| ||||
C、(-
| ||||
D、(-
|
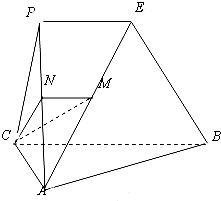如图，平面PAC⊥平面ABC，AC⊥BC，△PAC为等边三角形，PE∥BC，过BC作平面交AP、AE分别于点M、N．