题目内容
7.已知椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1(a>b>0)上一点A关于原点的对称点为点B,F为其右焦点,若AF⊥BF,设∠ABF=α,且α∈[$\frac{π}{6}$,$\frac{π}{4}$],则该椭圆离心率e的取值范围为( )
| A. | [$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$] | B. | [$\frac{\sqrt{2}}{2}$,1) | C. | [$\frac{\sqrt{2}}{2}$,$\sqrt{3}$-1] | D. | [$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{6}}{3}$] |
分析 由椭圆的定义及对称性求得丨AF丨+丨BF丨=2a,利用直角三角形的性质求得丨AF丨及丨BF丨,利用椭圆的离心率公式及正弦函数的图象及性质,即可求得e的取值范围.
解答 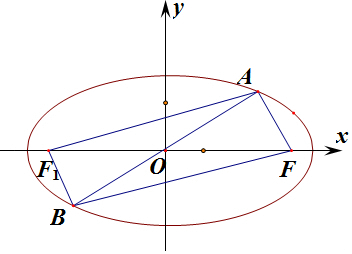 解:由已知,点B和点A关于原点对称,则点B也在椭圆上,
解:由已知,点B和点A关于原点对称,则点B也在椭圆上,
设椭圆的左焦点为F1,则根据椭圆定义:丨AF丨+丨AF1丨=2a=10,
根据椭圆对称性可知:丨AF1丨=丨BF丨,因此丨AF丨+丨BF丨=2a=10①;
因为AF⊥BF,则在Rt△ABF中,O为斜边AB中点,则丨AB丨=2丨OF丨=2c,那么丨AF丨=2csinα②,丨BF丨=2ccosα③;
将②、③代入①得,2csinα+2ccosα=2a,
则离心率e=$\frac{c}{a}$=$\frac{1}{sinα+cosα}$=$\frac{1}{\sqrt{2}sin(α+\frac{π}{4})}$,
由α∈[$\frac{π}{6}$,$\frac{π}{4}$],α+$\frac{π}{4}$∈[$\frac{5π}{12}$,$\frac{π}{2}$],
由sin$\frac{5π}{12}$=$\frac{\sqrt{6}+\sqrt{2}}{4}$,
由函数的单调性可知:sin(α+$\frac{π}{4}$)∈[$\frac{\sqrt{6}+\sqrt{2}}{4}$,1],则e∈[$\frac{\sqrt{2}}{2}$,$\sqrt{3}$-1],
故选:C.
点评 本题考查椭圆的定义,三角函数关系式的恒等变换,利用定义域求三角函数的值域,离心率公式的应用,属于中档题.

练习册系列答案
相关题目
17.命题“?x0∈R,x03-x02+1>0”的否定是( )
| A. | ?x0∈R,x${\;}_{0}^{3}$-x${\;}_{0}^{2}$+1<0 | B. | ?x∈R,x3-x2+1≤0 | ||
| C. | ?x0∈R,x${\;}_{0}^{3}$-x${\;}_{0}^{2}$+1≤0 | D. | ?x∈R,x3-x2+1>0 |
18.用数学归纳法证明不等式“$\frac{1}{n+1}+\frac{1}{n+2}+…+\frac{1}{2n}>\frac{13}{24}(n>2)$”时的过程中,由n=k到n=k+1,(k>2)时,不等式的左边( )
| A. | 增加了一项$\frac{1}{2(k+1)}$ | |
| B. | 增加了两项$\frac{1}{2k+1}+\frac{1}{2(k+1)}$ | |
| C. | 增加了一项$\frac{1}{2(k+1)}$,又减少了一项$\frac{1}{k+1}$ | |
| D. | 增加了两项$\frac{1}{2k+1}+\frac{1}{2(k+1)}$,又减少了一项$\frac{1}{k+1}$ |
2.统计某产品的广告费用x与销售额y的一组数据如表:
若根据如表提供的数据用最小二乘法可求得y对x的回归直线方程是$\stackrel{∧}{y}$=1.1x+4.6,则数据中的m的值应该是8.
| 广告费用x | 2 | 3 | 5 | 6 |
| 销售额y | 7 | m | 9 | 12 |
12.从4款甲型和5款乙型智能手机中任取3款,其中至少要甲乙型号各一款,则不同的取法共有( )
| A. | 140种 | B. | 80种 | C. | 70种 | D. | 35种 |
17.已知集合A={x|x(x-2)=0},B={x∈Z|4x2-9≤0},则A∪B等于( )
| A. | {-2,-1,0,1} | B. | {-1,0,1,2} | C. | [-2,2] | D. | {0,2} |
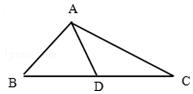 如图,在△ABC中,BC边上的中线AD长为3,且BD=2,sinB=$\frac{3\sqrt{6}}{8}$.
如图,在△ABC中,BC边上的中线AD长为3,且BD=2,sinB=$\frac{3\sqrt{6}}{8}$.