题目内容
7.某高中学校为展示学生的青春风采,举办了校园歌手大赛,该大赛分为预赛和决赛两个阶段,参加决赛的学生按照抽签方式决定出场顺序,通过预赛,选拔出甲、乙等5名学生参加决赛.(I)求决赛中学生甲、乙恰好排在前两位的概率;
(Ⅱ)若决赛中学生甲和学生乙之间间隔的人数记为X,求X的分布列及数学期望EX.
分析 (Ⅰ)设“学生甲、乙恰好排在前两位”为事件A,先求出基本事件总数n=${A}_{5}^{5}$,再求出决赛中学生甲、乙恰好排在前两位包含听基本事件个数,由此能求出决赛中学生甲、乙恰好排在前两位的概率.
(Ⅱ)随机变量X的可能的值为0,1,2,3.分别求出相应的概率,由此能求出随机变量X的分布列及数学期望EX.
解答 解:(Ⅰ)设“学生甲、乙恰好排在前两位”为事件A,
则$P(A)=\frac{A_2^2A_3^3}{A_5^5}=\frac{1}{10}$.(3分)
(Ⅱ)随机变量X的可能的值为0,1,2,3.(4分)
$P(X=0)=\frac{C_2^1A_4^4}{A_5^5}=\frac{2}{5}$,(5分)
$P(X=1)=\frac{C_3^1C_2^1A_3^3}{A_5^5}=\frac{3}{10}$,(7分)
$P(X=2)=\frac{C_3^2C_2^1C_2^1A_2^2}{A_5^5}=\frac{1}{5}$,(9分)
$P(X=3)=\frac{C_2^1A_3^3}{A_5^5}=\frac{1}{10}$.(10分)
随机变量X的分布列为
| X | 0 | 1 | 2 | 3 |
| P | $\frac{2}{5}$ | $\frac{3}{10}$ | $\frac{1}{5}$ | $\frac{1}{10}$ |
∴$EX=0×\frac{2}{5}+1×\frac{3}{10}+2×\frac{1}{5}+3×\frac{1}{10}=1$.(12分)
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.圆C与x轴相切于T(1,0),与y轴正半轴交于两点A、B,且|AB|=2,则圆C的标准方程为( )
| A. | (x-1)2+(y-$\sqrt{2}$)2=2 | B. | (x-1)2+(y-2)2=2 | C. | (x+1)2+(y+$\sqrt{2}$)2=4 | D. | (x-1)2+(y-$\sqrt{2}$)2=4 |
19.设方程5-x=|lgx|的两个根分别为x1,x2,则( )
| A. | x1x2<0 | B. | x1x2=1 | C. | x1x2>1 | D. | 0<x1x2<1 |
17.命题“?x0∈R,x03-x02+1>0”的否定是( )
| A. | ?x0∈R,x${\;}_{0}^{3}$-x${\;}_{0}^{2}$+1<0 | B. | ?x∈R,x3-x2+1≤0 | ||
| C. | ?x0∈R,x${\;}_{0}^{3}$-x${\;}_{0}^{2}$+1≤0 | D. | ?x∈R,x3-x2+1>0 |
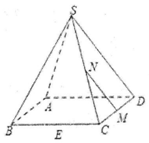 如图,在正四棱锥S-ABCD中,E.M.N分别是BC.CD.SC的中点,动点P的线段MN上运动时,下列四个结论:
如图,在正四棱锥S-ABCD中,E.M.N分别是BC.CD.SC的中点,动点P的线段MN上运动时,下列四个结论: