题目内容
设函数f(x)=
x3-
x2+bx+c,其中a>0.曲线y=f(x)在点P(0,f(0))处的切线方程为y=1.
(1)确定b,c的值;
(2)若过点(0,2)可作曲线y=f(x)的三条不同切线,求实数a的取值范围.
| 1 |
| 3 |
| a |
| 2 |
(1)确定b,c的值;
(2)若过点(0,2)可作曲线y=f(x)的三条不同切线,求实数a的取值范围.
考点:利用导数研究曲线上某点切线方程,导数的运算
专题:导数的概念及应用
分析:(1)先求f(x)的导数f'(x),再求f(0),由题意知f(0)=1,f'(0)=0,从而求出b,c的值;
(2)首先设出切点,求出切线的斜率,写出切线方程,代入点(0,2),得到关于x0的三次方程,且该方程有三个不同的实根,构造函数,运用导数求出极大值,令其值小于0,解出a的取值范围,注意a>0.
(2)首先设出切点,求出切线的斜率,写出切线方程,代入点(0,2),得到关于x0的三次方程,且该方程有三个不同的实根,构造函数,运用导数求出极大值,令其值小于0,解出a的取值范围,注意a>0.
解答:
解:(1)因为函数f(x)=
x3-
x2+bx+c,所以导数f'(x)=x2-ax+b,
又因为曲线y=f(x)在点P(0,f(0))处的切线方程为y=1,
所以f(0)=1,f'(0)=0,即b=0,c=1.
(2)由(1)知f(x)=
x3-
x2+1,f'(x)=x2-ax,
设切点为(x0,y0),
则y0=f(x0)=
x03-
x02+1,
切线的斜率为k=f'(x0)=x02-ax0
所以切线方程为y-y0=k(x-x0),
因为切线经过点(0,2),所以2-y0=-kx0,
即2-(
x03-
x02+1)=-(x02-ax0)x0
化简得:4x03-3ax02+6=0①,
因为过点(0,2)可作曲线y=f(x)的三条不同切线,
所以①有三个不同的实根.
即函数g(x)=4x3-3ax2+6有三个不同的零点.
导数g'(x)=12x2-6ax=0得x=0,或x=
(a>0)
可知只要极小值g(
)<0即4×
-3a•
+6<0,
所以a>2
.
故实数a的取值范围是(2
,+∞)
| 1 |
| 3 |
| a |
| 2 |
又因为曲线y=f(x)在点P(0,f(0))处的切线方程为y=1,
所以f(0)=1,f'(0)=0,即b=0,c=1.
(2)由(1)知f(x)=
| 1 |
| 3 |
| a |
| 2 |
设切点为(x0,y0),
则y0=f(x0)=
| 1 |
| 3 |
| a |
| 2 |
切线的斜率为k=f'(x0)=x02-ax0
所以切线方程为y-y0=k(x-x0),
因为切线经过点(0,2),所以2-y0=-kx0,
即2-(
| 1 |
| 3 |
| a |
| 2 |
化简得:4x03-3ax02+6=0①,
因为过点(0,2)可作曲线y=f(x)的三条不同切线,
所以①有三个不同的实根.
即函数g(x)=4x3-3ax2+6有三个不同的零点.
导数g'(x)=12x2-6ax=0得x=0,或x=
| a |
| 2 |
可知只要极小值g(
| a |
| 2 |
| a3 |
| 8 |
| a2 |
| 4 |
所以a>2
| 3 | 3 |
故实数a的取值范围是(2
| 3 | 3 |
点评:本题主要考查导数的概念及应用:求极值,解题中必须注意过某点的切线与在某点处的切线的区别,本题就是一个很好的例子,同时考查了字母的运算能力,是一道中档题.

练习册系列答案
相关题目
已知x,y∈R*,且x+y+
+
=5,则x+y的最大值是( )
| 1 |
| x |
| 1 |
| y |
| A、3 | B、3.5 | C、4 | D、4.5 |
已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2-2x,则f(x)在R上的表达式是( )
| A、y=x(x-2) |
| B、y=x(|x|-1) |
| C、y=|x|(x-2) |
| D、y=x(|x|-2) |
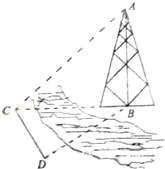 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个侧点C与D.现测得∠BCD=60°,∠BDC=75°,CD=50
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个侧点C与D.现测得∠BCD=60°,∠BDC=75°,CD=50