题目内容
7．已知空间中的直线m、n和平面α，且m⊥α．则“m⊥n”是“n?α”成立的（ ）| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
分析 m⊥α，n?α⇒m⊥n，反之不成立，可能n∥α．即可判断出结论．
解答 解：∵m⊥α，n?α⇒m⊥n，反之不成立，可能n∥α．
∴“m⊥n”是“n?α”成立的必要不充分条件．
故选：B．
点评 本题考查了空间线面垂直的判定与性质定理、简易逻辑的判定方法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
17．已知函数f（x）在定义域R上单调递减，且函数y=f（x-1）的图象关于点A（1，0）对称．若实数t满足f（t2-2t）+f（-3）＞0，则$\frac{t-1}{t-3}$的取值范围是 （ ）
| A． | （$\frac{1}{2}$，+∞） | B． | （-∞，$\frac{1}{2}$） | C． | （0，$\frac{2}{3}$） | D． | （$\frac{1}{2}$，1）∪（1，+∞） |
15．已知集合A={x||x-2|＜3，x∈Z}，B={0，1，2}，则集合A∩B=（ ）
| A． | {0，1，2} | B． | {0，1，2，3} | C． | {0，1} | D． | {1，2} |
2．将一颗骰子先后抛掷2次，观察向上的点数，则所得的两个点数和不小于10的概率为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{5}{18}$ | C． | $\frac{2}{9}$ | D． | $\frac{1}{6}$ |
12．
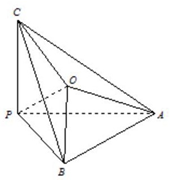如图，在三棱锥P-ABC中，∠APB=∠BPC=∠APC=90°，O在△ABC内，∠OPC=45°，∠OPA=60°，则∠OPB的余弦值为（ ）
如图，在三棱锥P-ABC中，∠APB=∠BPC=∠APC=90°，O在△ABC内，∠OPC=45°，∠OPA=60°，则∠OPB的余弦值为（ ）| A． | $\frac{\sqrt{3}}{2}$ | B． | $\frac{\sqrt{6}}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{\sqrt{2}}{2}$ |
16．设A为圆（x-1）2+y2=1上的动点，PA是圆的切线，且|PA|=1，则点P的轨迹方程是（ ）
| A． | （x-1）2+y2=2 | B． | （x-1）2+y2=4 | C． | y2=2x | D． | y2=-2x |
11．设函数$f（x）=\left\{\begin{array}{l}{log}_{\frac{1}{2}}^{（-x）}，x＜0\\{log}_{2}^{x}，x＞0\end{array}\right.$，若f（a）＞f（-a），则a的范围为（ ）
| A． | （-1，0）∪（0，1） | B． | （-1，0）∪（1，+∞） | C． | （-∞，-1）∪（1，+∞） | D． | （-∞，-1）∪（0，1） |