题目内容
19.已知函数f(x)=-sin2x+sinx+a,(1)当f(x)=0有实数解时,求a的取值范围;
(2)若$x∈[\frac{π}{6},\frac{2π}{3}]$,恒有1≤f(x)≤$\frac{17}{4}$,求a的取值范围.
分析 (1)由题意可转化为a=sin2x-sinx有解,(-1≤sinx≤1),通过求解函数y=sin2x-sinx(-1≤sinx≤1)的值域确定a的范围;
(2)把sinx看成一个整体,求出函数f(x)的值域为[a,a+$\frac{1}{4}$],再根据题意得[a,a+$\frac{1}{4}$]⊆[1,$\frac{17}{4}$],即可求出a的范围.
解答 解:(1)∵sinx∈[-1,1]
若f(x)=0有实数解⇒a=sin2x-sinx=(sinx-$\frac{1}{2}$)2-$\frac{1}{4}$有解
y=sin2x-sinx在区间[-1,$\frac{1}{2}$]上单调递减,[$\frac{1}{2}$,1]上单调递增
从而y=(sinx-$\frac{1}{2}$)2-$\frac{1}{4}$∈[-$\frac{1}{4}$,2],
∴a∈[-$\frac{1}{4}$,2];
(2)f(x)=-sin2x+sinx+a
=-(sinx-$\frac{1}{2}$)2+a+$\frac{1}{4}$.
由$x∈[\frac{π}{6},\frac{2π}{3}]$,$\frac{1}{2}$≤sinx≤1可以的出函数f(x)的值域为[a,a+$\frac{1}{4}$],
由1≤f(x)≤$\frac{17}{4}$得[a,a+$\frac{1}{4}$]⊆[1,$\frac{17}{4}$].
∴$\left\{\begin{array}{l}{a≥1}\\{a+\frac{1}{4}≤\frac{17}{4}}\end{array}\right.$⇒1≤a≤4,
故a的范围是1≤a≤4.
点评 本题主要以正弦函数的值域为载体,考查二次函数在闭区间上的值域,属于中档题.

| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
| A. | 横坐标缩短到原来的$\frac{1}{2}$倍(纵坐标不变),再向左平行移动$\frac{π}{8}$个单位长度 | |
| B. | 横坐标缩短到原来的$\frac{1}{2}$倍(纵坐标不变),再向左平行移动$\frac{π}{4}$个单位长度 | |
| C. | 横坐标伸长到原来的2倍(纵坐标不变),再向左平行移动$\frac{π}{8}$个单位长度 | |
| D. | 横坐标伸长到原来的2倍(纵坐标不变),再向左平行移动$\frac{π}{4}$个单位长度 |
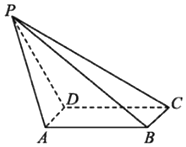 如图,在四棱锥P-ABCD中,底面ABCD是矩形,AD⊥PD,BC=1,PC=2$\sqrt{3}$,PD=CD=2,则二面角A-PB-C的正切值为$\frac{\sqrt{15}}{9}$.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,AD⊥PD,BC=1,PC=2$\sqrt{3}$,PD=CD=2,则二面角A-PB-C的正切值为$\frac{\sqrt{15}}{9}$.