题目内容
4.已知在△ABC中,角A,B,C所对的边分别为a,b,c,已知$\sqrt{2}$c-ccosA=acosC.(Ⅰ)求$\frac{b}{c}$的值;
(Ⅱ)若b+c=$\sqrt{2}$+1,a=$\sqrt{3}$,求△ABC的面积S.
分析 (I)由$\sqrt{2}$c-ccosA=acosC,利用正弦定理可得$\sqrt{2}$sinC=sinCcosA+sinAcosC=sin(A+C)=sinB,再利用正弦定理即可得出.
(II)由b+c=$\sqrt{2}$+1,$\frac{b}{c}$=$\sqrt{2}$.解得b,c.利用勾股定理的逆定理可得A为直角.即可得出面积.
解答 解:(I)∵$\sqrt{2}$c-ccosA=acosC,∴$\sqrt{2}$sinC=sinCcosA+sinAcosC=sin(A+C)=sinB,∴$\sqrt{2}$c=b.
∴$\frac{b}{c}$=$\sqrt{2}$.
(II)由b+c=$\sqrt{2}$+1,$\frac{b}{c}$=$\sqrt{2}$.解得b=$\sqrt{2}$,c=1.
a=$\sqrt{3}$,∴b2+c2=a2.∴A=$\frac{π}{2}$
∴△ABC的面积S=$\frac{1}{2}×1×\sqrt{2}$=$\frac{\sqrt{2}}{2}$.
点评 本题考查了正弦定理、和差公式、勾股定理的逆定理、三角函数求值、三角形面积,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
20.某商场拟对商品进行促销,现有两种方案供选择.每种促销方案都需分两个月实施,且每种方案中第一个月与第二个月的销售相互独立.根据以往促销的统计数据,若实施方案1,顶计第一个月的销量是促销前的1.2倍和1.5倍的概率分别是0.6和0.4.第二个月销量是笫一个月的1.4倍和1.6倍的概率都是0.5;若实施方案2,预计第一个月的销量是促销前的1.4倍和1.5倍的概率分别是0.7和0.3,第二个月的销量是第一个月的1.2倍和1.6倍的概率分别是0.6和0.4.令ξi(i=1,2)表示实施方案i的第二个月的销量是促销前销量的倍数.
(Ⅰ)求ξ1,ξ2的分布列:
(Ⅱ)不管实施哪种方案,ξi与第二个月的利润之间的关系如表,试比较哪种方案第二个月的利润更大.
(Ⅰ)求ξ1,ξ2的分布列:
(Ⅱ)不管实施哪种方案,ξi与第二个月的利润之间的关系如表,试比较哪种方案第二个月的利润更大.
| 销量倍数 | ξi≤1.7 | 1.7<ξi<2.3 | ξi2.3 |
| 利润(万元) | 15 | 20 | 25 |
1.若a=log23,b=log3$\frac{1}{2}$,c=3-2,则下列结论正确的是( )
| A. | a<c<b | B. | c<a<b | C. | b<c<a | D. | c<b<a |
12.设{an}是等差数列,{bn}是等比数列,且a1=b1=1,a2017=b2017=2017,则下列结论正确的是( )
| A. | a1008>a1009 | B. | a2016<b2016 | ||
| C. | ?n∈N*,1<n<2017,an>bn | D. | ?n∈N*,1<n<2017,使得an=bn |
19.甲、乙两人可参加A,B,C三个不同的学习小组,若每人必须参加并且仅能参加一个学习小组,则两人参加同一个学习小组的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
9.在(x-2)6展开式中,二项式系数的最大值为 a,含x5项的系数为b,则$\frac{a}{b}$=( )
| A. | $\frac{5}{3}$ | B. | $-\frac{5}{3}$ | C. | $\frac{3}{5}$ | D. | $-\frac{3}{5}$ |
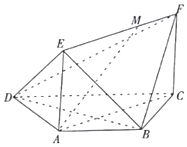 如图,在梯形ABCD中,AB∥DC,AD=AB=BC=1,$∠ADC=\frac{π}{3}$,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=1,点M在线段EF上.
如图,在梯形ABCD中,AB∥DC,AD=AB=BC=1,$∠ADC=\frac{π}{3}$,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=1,点M在线段EF上.