题目内容
18.已知x,y满足条件$\left\{\begin{array}{l}1≤x+y≤3\\-1≤x-y≤1\end{array}\right.$(1)求2x-y的最小值;
(2)求x2+y2的最小值;
(3)求$\frac{y+1}{x+1}$的取值范围.
分析 画出约束条件的可行域,(1)判断目标函数的最优解求解即可.(2)利用目标函数的几何意义求解即可.(3)利用目标函数几何意义斜率故选求解即可.
解答 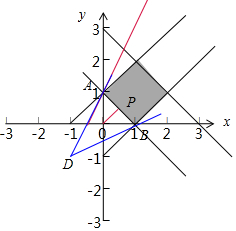 解:x,y满足条件$\left\{\begin{array}{l}1≤x+y≤3\\-1≤x-y≤1\end{array}\right.$的可行域如图:
解:x,y满足条件$\left\{\begin{array}{l}1≤x+y≤3\\-1≤x-y≤1\end{array}\right.$的可行域如图:
(1)平行直线z=2x-y,当直线经过可行域的A时,
z取得的最小值;-1.
(2)x2+y2的最小值,就是可行域的P与坐标原点的连线的距离的平方,转化为原点与x+y=1的距离的平方,$({\frac{1}{\sqrt{2}})}^{2}$=$\frac{1}{2}$;
(3)$\frac{y+1}{x+1}$的几何意义是可行域内的点与(-1,-1)连线的斜率,显然DB的斜率最小,DA的斜率最大,
kDB=$\frac{0+1}{1+1}$=$\frac{1}{2}$,kDA=$\frac{1+1}{0+1}$=2,
$\frac{y+1}{x+1}$的取值范围:$[{\frac{1}{2},2}]$.
点评 本题考查线性规划的简单应用,判断最优解以及目标函数的几何意义是解题的关键.考查数形结合思想的应用.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
9.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$的焦点在y轴上,a∈{1,2,3,4,5},b∈{1,2,3,4,5,6,7},则这样的椭圆有( )
| A. | 12个 | B. | 20个 | C. | 24个 | D. | 35个 |
6.方程${C}_{28}^{x}$=${C}_{28}^{3x-8}$的解为( )
| A. | 4 或9 | B. | 9 | C. | 4 | D. | 5 |
3.在△ABC中,角A,B,C所对的边分别为a,b,c,且a,2b,c成等差数列,则cosB的最小值为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{7}{8}$ |
7.已知条件p:a≤1,条件q:-1≤a≤1,则p是q的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 如图,△ABC在$\overrightarrow{CA}$=$\overrightarrow{a}$,$\overrightarrow{CB}$=$\overrightarrow{b}$,M,N分是$\overrightarrow{CA}$,$\overrightarrow{CB}$上的点,且$\overrightarrow{CM}$=$\frac{1}{3}$$\overrightarrow{a}$,$\overrightarrow{CN}$=$\frac{1}{2}$$\overrightarrow{b}$,设$\overrightarrow{AN}$与$\overrightarrow{BM}$ 交于P,用向量$\overrightarrow{a}$,$\overrightarrow{b}$ 表示向量$\overrightarrow{CP}$,并求出AP:PN,BP:PM.
如图,△ABC在$\overrightarrow{CA}$=$\overrightarrow{a}$,$\overrightarrow{CB}$=$\overrightarrow{b}$,M,N分是$\overrightarrow{CA}$,$\overrightarrow{CB}$上的点,且$\overrightarrow{CM}$=$\frac{1}{3}$$\overrightarrow{a}$,$\overrightarrow{CN}$=$\frac{1}{2}$$\overrightarrow{b}$,设$\overrightarrow{AN}$与$\overrightarrow{BM}$ 交于P,用向量$\overrightarrow{a}$,$\overrightarrow{b}$ 表示向量$\overrightarrow{CP}$,并求出AP:PN,BP:PM.